Question Number 54995 by peter frank last updated on 15/Feb/19
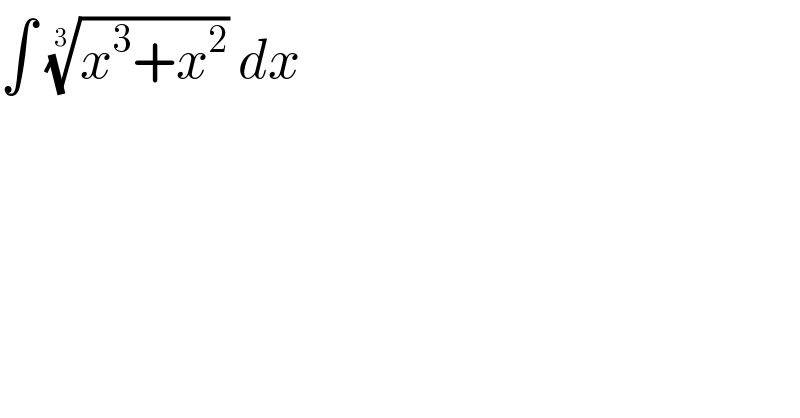
$$\int\:\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} }\:{dx} \\ $$
Commented by MJS last updated on 16/Feb/19

$$\mathrm{I}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{of}\:\mathrm{typing}\:\mathrm{work} \\ $$$$\mathrm{if}\:\mathrm{you}\:\mathrm{need}\:\mathrm{it}\:\mathrm{urgently}\:\mathrm{I}\:\mathrm{will}\:\mathrm{post}\:\mathrm{it} \\ $$
Commented by peter frank last updated on 16/Feb/19
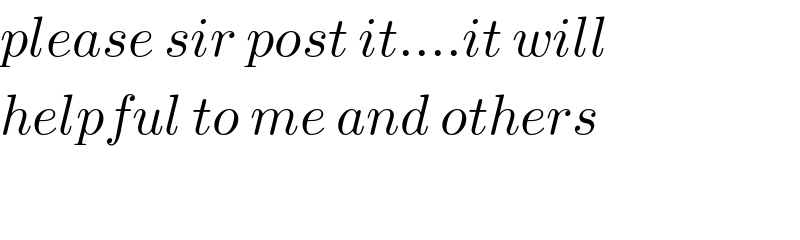
$${please}\:{sir}\:{post}\:{it}….{it}\:{will}\: \\ $$$${helpful}\:{to}\:{me}\:{and}\:{others} \\ $$$$ \\ $$
Commented by MJS last updated on 16/Feb/19
$$\mathrm{ok}\:\mathrm{might}\:\mathrm{take}\:\mathrm{some}\:\mathrm{time} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 16/Feb/19
![∫x^(2/3) (1+x)^(1/3) dx ∫x^(2/3) [1+(1/3)x+(1/3)((1/3)−1)(x^2 /(2!))+(1/3)((1/3)−1)((1/3)−2)(x^3 /(3!))+...]dx ∫x^(2/3) +(1/3)x^(5/3) +(1/3)((1/3)−1)x^(8/3) ×(1/(2!))+(1/3)((1/3)−1)((1/3)−2)(x^((11)/3) /(3!))+...]dx so in the form of... ∫x^(2/3) +a_1 x^(5/3) +a_2 x^(8/3) +a_3 x^((11)/3) +...dx (x^(5/3) /(5/3))+a_1 ×(x^(8/3) /(8/3))+a_2 (x^((11)/3) /((11)/3))+....](https://www.tinkutara.com/question/Q55037.png)
$$\int{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} {dx} \\ $$$$\int{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \left[\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}{x}+\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}\right)\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{2}\right)\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+…\right]{dx} \\ $$$$\left.\int{x}^{\frac{\mathrm{2}}{\mathrm{3}}} +\frac{\mathrm{1}}{\mathrm{3}}{x}^{\frac{\mathrm{5}}{\mathrm{3}}} +\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}\right){x}^{\frac{\mathrm{8}}{\mathrm{3}}} ×\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{2}\right)\frac{{x}^{\frac{\mathrm{11}}{\mathrm{3}}} }{\mathrm{3}!}+…\right]{dx} \\ $$$${so}\:{in}\:{the}\:{form}\:{of}… \\ $$$$\int{x}^{\frac{\mathrm{2}}{\mathrm{3}}} +{a}_{\mathrm{1}} {x}^{\frac{\mathrm{5}}{\mathrm{3}}} +{a}_{\mathrm{2}} {x}^{\frac{\mathrm{8}}{\mathrm{3}}} +{a}_{\mathrm{3}} {x}^{\frac{\mathrm{11}}{\mathrm{3}}} +…{dx} \\ $$$$\frac{{x}^{\frac{\mathrm{5}}{\mathrm{3}}} }{\frac{\mathrm{5}}{\mathrm{3}}}+{a}_{\mathrm{1}} ×\frac{{x}^{\frac{\mathrm{8}}{\mathrm{3}}} }{\frac{\mathrm{8}}{\mathrm{3}}}+{a}_{\mathrm{2}} \frac{{x}^{\frac{\mathrm{11}}{\mathrm{3}}} }{\frac{\mathrm{11}}{\mathrm{3}}}+…. \\ $$
