Question Number 112360 by bemath last updated on 07/Sep/20
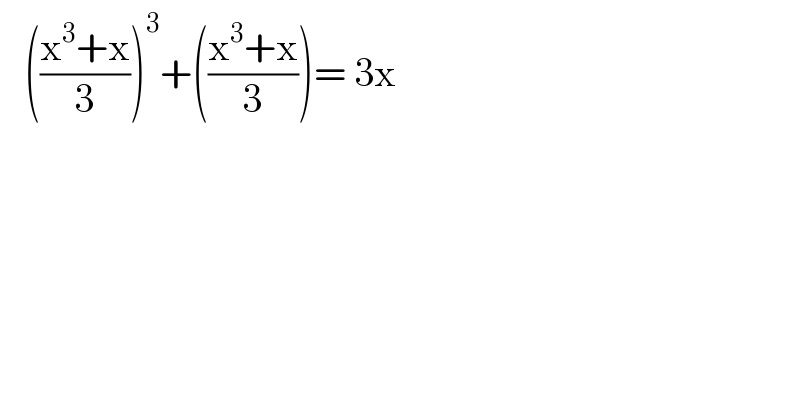
$$\:\:\:\left(\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{x}}{\mathrm{3}}\right)^{\mathrm{3}} +\left(\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{x}}{\mathrm{3}}\right)=\:\mathrm{3x}\: \\ $$
Commented by john santu last updated on 07/Sep/20
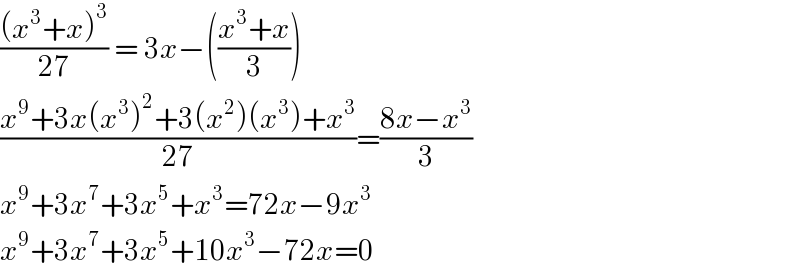
$$\frac{\left({x}^{\mathrm{3}} +{x}\right)^{\mathrm{3}} }{\mathrm{27}}\:=\:\mathrm{3}{x}−\left(\frac{{x}^{\mathrm{3}} +{x}}{\mathrm{3}}\right) \\ $$$$\frac{{x}^{\mathrm{9}} +\mathrm{3}{x}\left({x}^{\mathrm{3}} \right)^{\mathrm{2}} +\mathrm{3}\left({x}^{\mathrm{2}} \right)\left({x}^{\mathrm{3}} \right)+{x}^{\mathrm{3}} }{\mathrm{27}}=\frac{\mathrm{8}{x}−{x}^{\mathrm{3}} }{\mathrm{3}} \\ $$$${x}^{\mathrm{9}} +\mathrm{3}{x}^{\mathrm{7}} +\mathrm{3}{x}^{\mathrm{5}} +{x}^{\mathrm{3}} =\mathrm{72}{x}−\mathrm{9}{x}^{\mathrm{3}} \\ $$$${x}^{\mathrm{9}} +\mathrm{3}{x}^{\mathrm{7}} +\mathrm{3}{x}^{\mathrm{5}} +\mathrm{10}{x}^{\mathrm{3}} −\mathrm{72}{x}=\mathrm{0} \\ $$
Answered by MJS_new last updated on 07/Sep/20
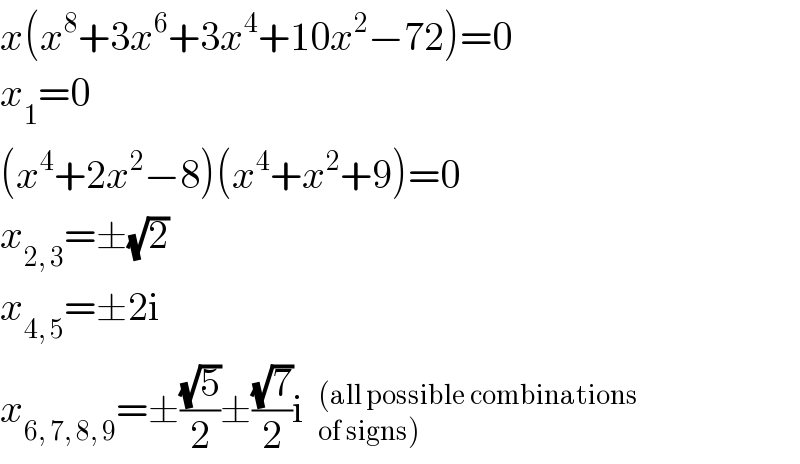
$${x}\left({x}^{\mathrm{8}} +\mathrm{3}{x}^{\mathrm{6}} +\mathrm{3}{x}^{\mathrm{4}} +\mathrm{10}{x}^{\mathrm{2}} −\mathrm{72}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{0} \\ $$$$\left({x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{8}\right)\left({x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{9}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{2},\:\mathrm{3}} =\pm\sqrt{\mathrm{2}} \\ $$$${x}_{\mathrm{4},\:\mathrm{5}} =\pm\mathrm{2i} \\ $$$${x}_{\mathrm{6},\:\mathrm{7},\:\mathrm{8},\:\mathrm{9}} =\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{i} \\ $$
Commented by malwan last updated on 07/Sep/20
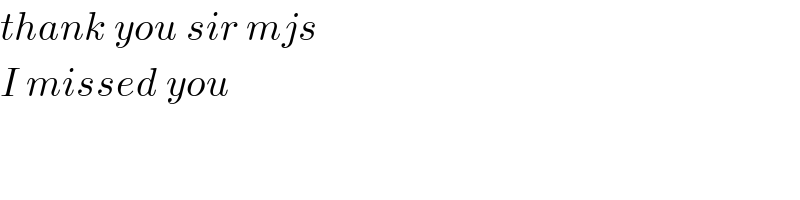
$${thank}\:{you}\:{sir}\:{mjs} \\ $$$${I}\:{missed}\:{you}\: \\ $$
Commented by MJS_new last updated on 07/Sep/20
$$\mathrm{You}'\mathrm{re}\:\mathrm{welcome}!\:\mathrm{I}\:\mathrm{also}\:\mathrm{missed}\:\mathrm{you}\:\&\:\mathrm{everybody} \\ $$$$\mathrm{here}… \\ $$
