Question Number 41084 by Tawa1 last updated on 01/Aug/18
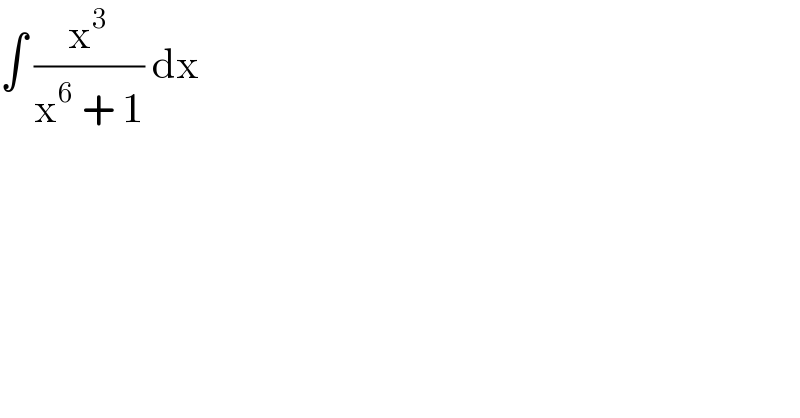
$$\int\:\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{6}} \:+\:\mathrm{1}}\:\mathrm{dx} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Aug/18
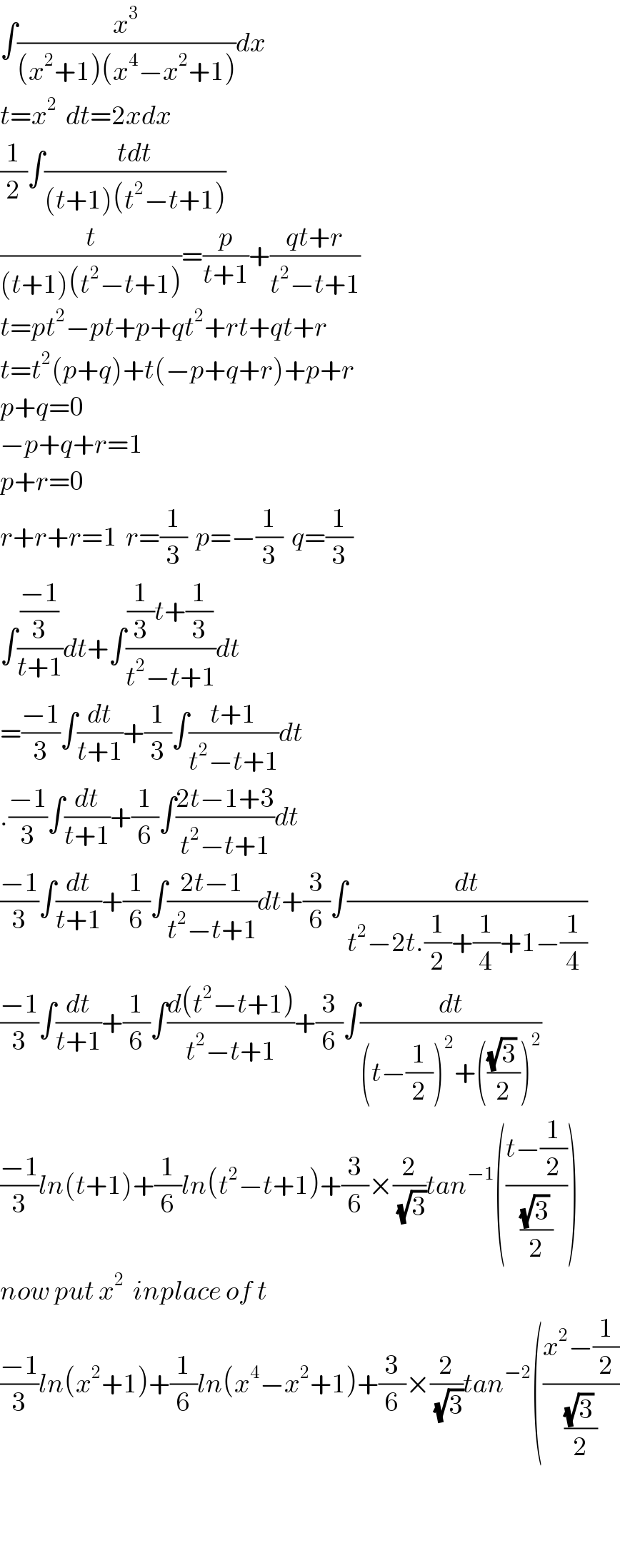
$$\int\frac{{x}^{\mathrm{3}} }{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)}{dx} \\ $$$${t}={x}^{\mathrm{2}} \:\:{dt}=\mathrm{2}{xdx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{tdt}}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)} \\ $$$$\frac{{t}}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)}=\frac{{p}}{{t}+\mathrm{1}}+\frac{{qt}+{r}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}} \\ $$$${t}={pt}^{\mathrm{2}} −{pt}+{p}+{qt}^{\mathrm{2}} +{rt}+{qt}+{r} \\ $$$${t}={t}^{\mathrm{2}} \left({p}+{q}\right)+{t}\left(−{p}+{q}+{r}\right)+{p}+{r} \\ $$$${p}+{q}=\mathrm{0} \\ $$$$−{p}+{q}+{r}=\mathrm{1} \\ $$$${p}+{r}=\mathrm{0} \\ $$$${r}+{r}+{r}=\mathrm{1}\:\:{r}=\frac{\mathrm{1}}{\mathrm{3}}\:\:{p}=−\frac{\mathrm{1}}{\mathrm{3}}\:\:{q}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\int\frac{\frac{−\mathrm{1}}{\mathrm{3}}}{{t}+\mathrm{1}}{dt}+\int\frac{\frac{\mathrm{1}}{\mathrm{3}}{t}+\frac{\mathrm{1}}{\mathrm{3}}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}{dt} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{3}}\int\frac{{dt}}{{t}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}{dt} \\ $$$$.\frac{−\mathrm{1}}{\mathrm{3}}\int\frac{{dt}}{{t}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{6}}\int\frac{\mathrm{2}{t}−\mathrm{1}+\mathrm{3}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}{dt} \\ $$$$\frac{−\mathrm{1}}{\mathrm{3}}\int\frac{{dt}}{{t}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{6}}\int\frac{\mathrm{2}{t}−\mathrm{1}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}{dt}+\frac{\mathrm{3}}{\mathrm{6}}\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{2}{t}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\frac{−\mathrm{1}}{\mathrm{3}}\int\frac{{dt}}{{t}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{d}\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}+\frac{\mathrm{3}}{\mathrm{6}}\int\frac{{dt}}{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}\:}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\frac{−\mathrm{1}}{\mathrm{3}}{ln}\left({t}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{6}}{ln}\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)+\frac{\mathrm{3}}{\mathrm{6}}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\frac{{t}−\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}\:}{\mathrm{2}}}\right) \\ $$$${now}\:{put}\:{x}^{\mathrm{2}} \:\:{inplace}\:{of}\:{t} \\ $$$$\frac{−\mathrm{1}}{\mathrm{3}}{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{6}}{ln}\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)+\frac{\mathrm{3}}{\mathrm{6}}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{2}} \left(\frac{{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}\:}{\mathrm{2}}}\right. \\ $$$$ \\ $$$$ \\ $$
Commented by Tawa1 last updated on 01/Aug/18
$$\mathrm{Wow}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 01/Aug/18

$${good}\:{night}… \\ $$
