Menu Close

x-3-x-6-8y-y-3-y-6-8z-z-3-z-6-8x-x-y-z-

Tinku Tara 0 Comments
Pin




Question Number 163906 by HongKing last updated on 11/Jan/22
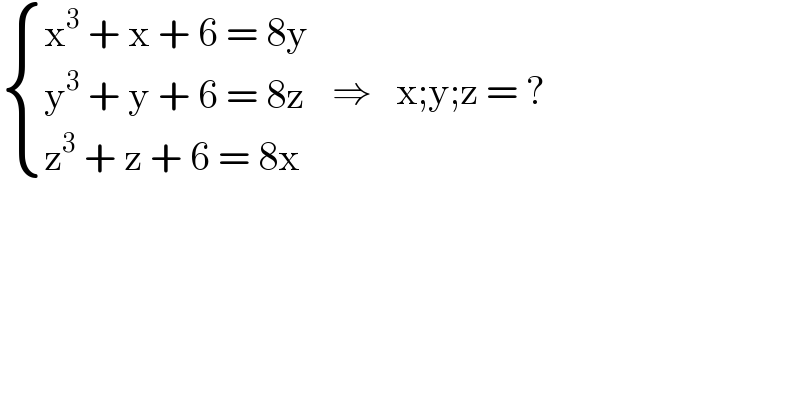
{ ((x^3 + x + 6 = 8y)),((y^3 + y + 6 = 8z)),((z^3 + z + 6 = 8x)) :} ⇒ x;y;z = ?
$$\begin{cases}{\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{x}\:+\:\mathrm{6}\:=\:\mathrm{8y}}\\{\mathrm{y}^{\mathrm{3}} \:+\:\mathrm{y}\:+\:\mathrm{6}\:=\:\mathrm{8z}}\\{\mathrm{z}^{\mathrm{3}} \:+\:\mathrm{z}\:+\:\mathrm{6}\:=\:\mathrm{8x}}\end{cases}\:\:\:\Rightarrow\:\:\:\mathrm{x};\mathrm{y};\mathrm{z}\:=\:? \\ $$
Answered by ajfour last updated on 11/Jan/22
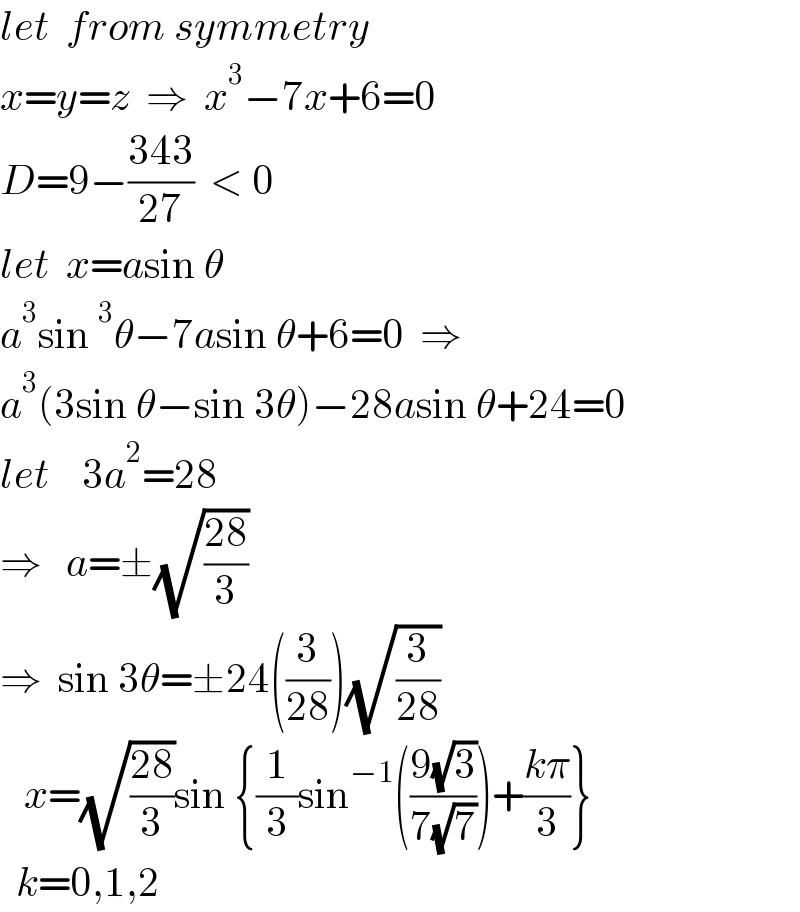
let from symmetry x=y=z ⇒ x^3 −7x+6=0 D=9−((343)/(27)) < 0 let x=asin θ a^3 sin^3 θ−7asin θ+6=0 ⇒ a^3 (3sin θ−sin 3θ)−28asin θ+24=0 let 3a^2 =28 ⇒ a=±(√((28)/3)) ⇒ sin 3θ=±24((3/(28)))(√(3/(28))) x=(√((28)/3))sin {(1/3)sin^(−1) (((9(√3))/(7(√7))))+((kπ)/3)} k=0,1,2
$${let}\:\:{from}\:{symmetry} \\ $$$${x}={y}={z}\:\:\Rightarrow\:\:{x}^{\mathrm{3}} −\mathrm{7}{x}+\mathrm{6}=\mathrm{0} \\ $$$${D}=\mathrm{9}−\frac{\mathrm{343}}{\mathrm{27}}\:\:<\:\mathrm{0} \\ $$$${let}\:\:{x}={a}\mathrm{sin}\:\theta \\ $$$${a}^{\mathrm{3}} \mathrm{sin}\:^{\mathrm{3}} \theta−\mathrm{7}{a}\mathrm{sin}\:\theta+\mathrm{6}=\mathrm{0}\:\:\Rightarrow \\ $$$${a}^{\mathrm{3}} \left(\mathrm{3sin}\:\theta−\mathrm{sin}\:\mathrm{3}\theta\right)−\mathrm{28}{a}\mathrm{sin}\:\theta+\mathrm{24}=\mathrm{0} \\ $$$${let}\:\:\:\:\mathrm{3}{a}^{\mathrm{2}} =\mathrm{28} \\ $$$$\Rightarrow\:\:\:{a}=\pm\sqrt{\frac{\mathrm{28}}{\mathrm{3}}} \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\mathrm{3}\theta=\pm\mathrm{24}\left(\frac{\mathrm{3}}{\mathrm{28}}\right)\sqrt{\frac{\mathrm{3}}{\mathrm{28}}} \\ $$$$\:\:\:{x}=\sqrt{\frac{\mathrm{28}}{\mathrm{3}}}\mathrm{sin}\:\left\{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{9}\sqrt{\mathrm{3}}}{\mathrm{7}\sqrt{\mathrm{7}}}\right)+\frac{{k}\pi}{\mathrm{3}}\right\} \\ $$$$\:\:{k}=\mathrm{0},\mathrm{1},\mathrm{2} \\ $$
Commented by mr W last updated on 11/Jan/22
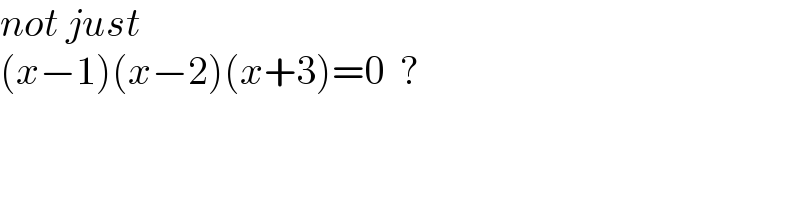
not just (x−1)(x−2)(x+3)=0 ?
$${not}\:{just}\: \\ $$$$\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}+\mathrm{3}\right)=\mathrm{0}\:\:? \\ $$
Commented by ajfour last updated on 11/Jan/22
⇒ x^3 −7x+6=0 yes for sure.
$$\Rightarrow\:\:{x}^{\mathrm{3}} −\mathrm{7}{x}+\mathrm{6}=\mathrm{0} \\ $$$${yes}\:{for}\:{sure}. \\ $$
Commented by mr W last updated on 11/Jan/22
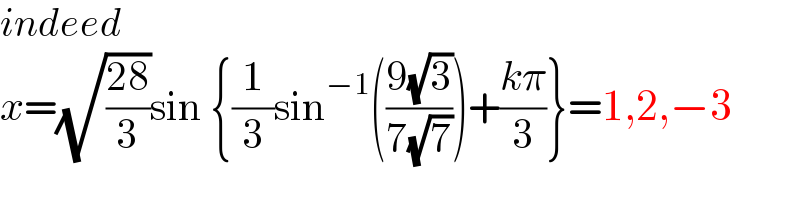
indeed x=(√((28)/3))sin {(1/3)sin^(−1) (((9(√3))/(7(√7))))+((kπ)/3)}=1,2,−3
$${indeed} \\ $$$${x}=\sqrt{\frac{\mathrm{28}}{\mathrm{3}}}\mathrm{sin}\:\left\{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{9}\sqrt{\mathrm{3}}}{\mathrm{7}\sqrt{\mathrm{7}}}\right)+\frac{{k}\pi}{\mathrm{3}}\right\}=\mathrm{1},\mathrm{2},−\mathrm{3} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *