Question Number 78878 by M±th+et£s last updated on 21/Jan/20
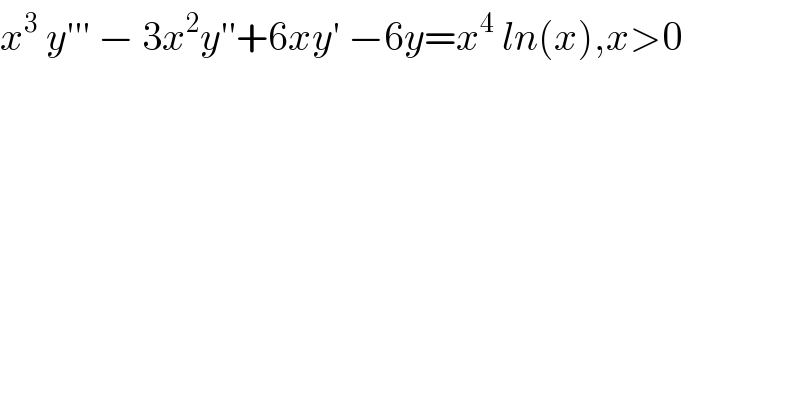
$${x}^{\mathrm{3}} \:{y}'''\:−\:\mathrm{3}{x}^{\mathrm{2}} {y}''+\mathrm{6}{xy}'\:−\mathrm{6}{y}={x}^{\mathrm{4}} \:{ln}\left({x}\right),{x}>\mathrm{0} \\ $$
Answered by mind is power last updated on 21/Jan/20

$${y}={x}^{{a}} \:{Solution}\:{of}\:{homgenius}\Rightarrow \\ $$$${x}^{\mathrm{3}} {y}'''−\mathrm{3}{x}^{\mathrm{2}} {y}''+\mathrm{6}{xy}'−\mathrm{6}{y} \\ $$$$\left({a}\left({a}−\mathrm{1}\right)\left({a}−\mathrm{2}\right)−\mathrm{3}{a}\left({a}−\mathrm{1}\right)+\mathrm{6}{a}−\mathrm{6}\right){y}\left({x}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\left({a}−\mathrm{1}\right)\left({a}\left({a}−\mathrm{2}\right)−\mathrm{3}{a}+\mathrm{6}\right)=\mathrm{0} \\ $$$$\left({a}−\mathrm{1}\right)\left({a}^{\mathrm{2}} −\mathrm{5}{a}+\mathrm{6}\right)=\mathrm{0} \\ $$$$\Rightarrow\left({a}−\mathrm{1}\right)\left({a}−\mathrm{3}\right)\left({a}−\mathrm{2}\right) \\ $$$$\Rightarrow{a}\in\left\{\mathrm{1},\mathrm{2},\mathrm{3}\right\} \\ $$$${y}_{\mathrm{1}} ={x},{y}_{\mathrm{2}} ={x}^{\mathrm{2}} ,{y}_{\mathrm{3}} ={x}^{\mathrm{3}} \:,{y}_{\mathrm{1}} ,{y}_{\mathrm{2}} ,{y}_{\mathrm{3}} \mathrm{3}\:{independent}\:{Solution}\:\Rightarrow \\ $$$${Y}={ay}_{\mathrm{1}} +{by}_{\mathrm{2}} +{cy}_{\mathrm{3}} \:\:{Solution}\:{of}\:{Homgenius}\:{Equation} \\ $$$${let}\:{y}={g}\left({x}\right){x}\:{particular}\:{Solution} \\ $$$${y}'={xg}'+{g} \\ $$$${y}''=\mathrm{2}{g}'+{xg}'' \\ $$$${y}'''=\mathrm{3}{g}''+{xg}''' \\ $$$$\Rightarrow{x}^{\mathrm{3}} \left(\mathrm{3}{g}''+{xg}'''\right)−\mathrm{3}{x}^{\mathrm{2}} \left(\mathrm{2}{g}'+{xg}''\right)+\mathrm{6}{x}\left({xg}'+{g}\right)−\mathrm{6}{xg}\left({x}\right)={x}^{\mathrm{4}} {ln}\left({x}\right) \\ $$$$\Rightarrow{x}^{\mathrm{4}} {g}'''={x}^{\mathrm{4}} {ln}\left({x}\right)\Rightarrow{g}'''\left({x}\right)={ln}\left({x}\right) \\ $$$$\Rightarrow{g}''={xln}\left({x}\right)−{x} \\ $$$${g}'\left({x}\right)=\frac{{x}^{\mathrm{2}} {ln}\left({x}\right)}{\mathrm{2}}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}=\frac{{x}^{\mathrm{2}} {ln}\left({x}\right)}{\mathrm{2}}−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${g}\left({x}\right)=\frac{{x}^{\mathrm{3}} {ln}\left({x}\right)}{\mathrm{6}}−\frac{{x}^{\mathrm{3}} }{\mathrm{18}}−\frac{{x}^{\mathrm{3}} }{\mathrm{4}}=\frac{{x}^{\mathrm{3}} {ln}\left({x}\right)}{\mathrm{6}}−\frac{\mathrm{11}{x}^{\mathrm{3}} }{\mathrm{36}} \\ $$$${y}\left({x}\right)={ax}+{bx}^{\mathrm{2}} +{cx}^{\mathrm{3}} +\frac{{x}^{\mathrm{4}} }{\mathrm{6}}\left({ln}\left({x}\right)−\frac{\mathrm{11}}{\mathrm{6}}\right) \\ $$$$ \\ $$
Commented by M±th+et£s last updated on 21/Jan/20

$${god}\:{bless}\:{you}\:{sir} \\ $$$$ \\ $$
Commented by mind is power last updated on 21/Jan/20
$${Thanx}\:{you}\:{To}\:{sir} \\ $$
