Question Number 38384 by NECx last updated on 24/Jun/18

$$\int{x}^{−\mathrm{3}{cosx}} {dx} \\ $$$$ \\ $$$${please}\:{is}\:{this}\:{possible}? \\ $$$${If}\:{possibld}\:{then}\:{prove}\:{it}. \\ $$$$ \\ $$$${Thanks}\:{in}\:{advance}. \\ $$
Commented by prof Abdo imad last updated on 25/Jun/18
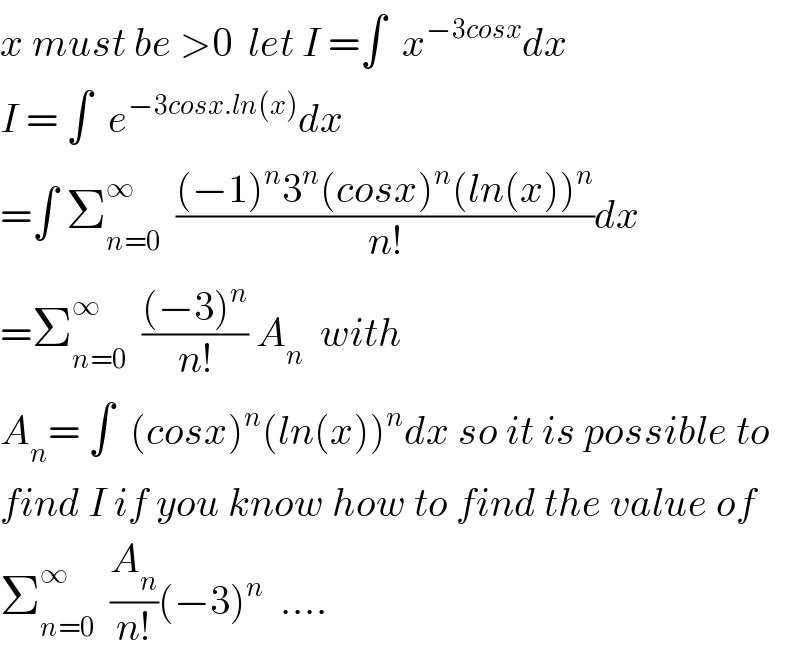
$${x}\:{must}\:{be}\:>\mathrm{0}\:\:{let}\:{I}\:=\int\:\:{x}^{−\mathrm{3}{cosx}} {dx} \\ $$$${I}\:=\:\int\:\:{e}^{−\mathrm{3}{cosx}.{ln}\left({x}\right)} {dx} \\ $$$$=\int\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} \mathrm{3}^{{n}} \left({cosx}\right)^{{n}} \left({ln}\left({x}\right)\right)^{{n}} }{{n}!}{dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{3}\right)^{{n}} }{{n}!}\:{A}_{{n}} \:\:{with} \\ $$$${A}_{{n}} =\:\int\:\:\left({cosx}\right)^{{n}} \left({ln}\left({x}\right)\right)^{{n}} {dx}\:{so}\:{it}\:{is}\:{possible}\:{to} \\ $$$${find}\:{I}\:{if}\:{you}\:{know}\:{how}\:{to}\:{find}\:{the}\:{value}\:{of} \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{A}_{{n}} }{{n}!}\left(−\mathrm{3}\right)^{{n}} \:\:…. \\ $$
