Question Number 157227 by amin96 last updated on 21/Oct/21
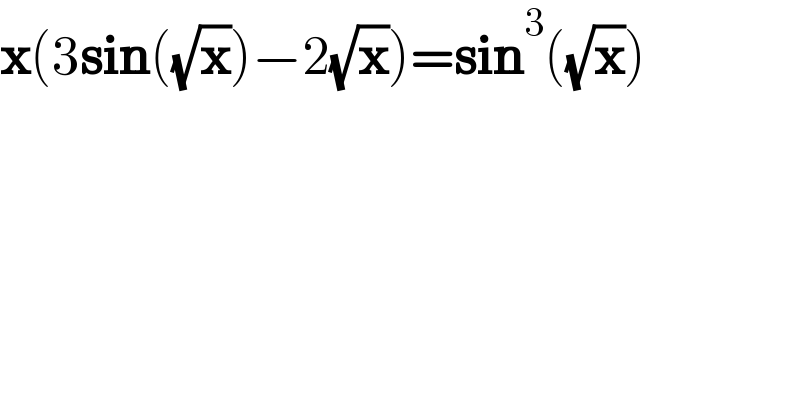
$$\boldsymbol{\mathrm{x}}\left(\mathrm{3}\boldsymbol{\mathrm{sin}}\left(\sqrt{\boldsymbol{\mathrm{x}}}\right)−\mathrm{2}\sqrt{\boldsymbol{\mathrm{x}}}\right)=\boldsymbol{\mathrm{sin}}^{\mathrm{3}} \left(\sqrt{\boldsymbol{\mathrm{x}}}\right) \\ $$
Answered by Javokhir last updated on 21/Oct/21
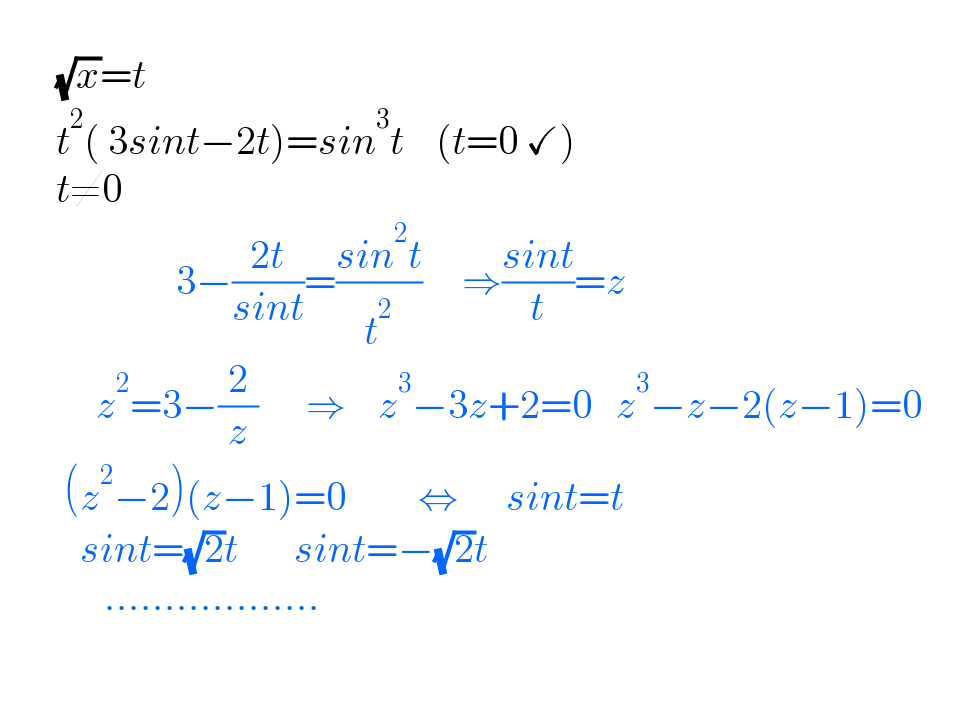
$$ \\ $$$$\:\:\:\:\:\:\:\sqrt{{x}}={t} \\ $$$$\:\:\:\:\:\:\:{t}^{\mathrm{2}} \left(\:\mathrm{3}{sint}−\mathrm{2}{t}\right)={sin}^{\mathrm{3}} {t}\:\:\:\:\left({t}=\mathrm{0}\:\checkmark\right) \\ $$$$\:\:\:\:\:\:\:{t}\neq\mathrm{0}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}−\frac{\mathrm{2}{t}}{{sint}}=\frac{{sin}^{\mathrm{2}} {t}}{{t}^{\mathrm{2}} }\:\:\:\:\:\Rightarrow\frac{{sint}}{{t}}={z} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{z}^{\mathrm{2}} =\mathrm{3}−\frac{\mathrm{2}}{{z}}\:\:\:\:\:\:\Rightarrow\:\:\:\:{z}^{\mathrm{3}} −\mathrm{3}{z}+\mathrm{2}=\mathrm{0}\:\:\:{z}^{\mathrm{3}} −{z}−\mathrm{2}\left({z}−\mathrm{1}\right)=\mathrm{0}\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\left({z}^{\mathrm{2}} −\mathrm{2}\right)\left({z}−\mathrm{1}\right)=\mathrm{0}\:\:\:\:\:\:\:\:\:\Leftrightarrow\:\:\:\:\:\:{sint}={t} \\ $$$$\:\:\:\:\:\:\:\:\:\:{sint}=\sqrt{\mathrm{2}}{t}\:\:\:\:\:\:\:{sint}=−\sqrt{\mathrm{2}}{t}\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:……………… \\ $$$$ \\ $$$$ \\ $$
