Question Number 34056 by Learner last updated on 30/Apr/18

$${x}^{\mathrm{3}{z}} =\mathrm{1}\: \\ $$$${x}^{\mathrm{2}} ={y} \\ $$$${z}={y}^{{n}} \\ $$$${FIND}\:{THE}\:{VALUE}\:{OF}\:{n} \\ $$$${please}\:{i}\:{need}\:{your}\:{help}\:{ASAP}.\:{thanks} \\ $$
Commented by math1967 last updated on 30/Apr/18
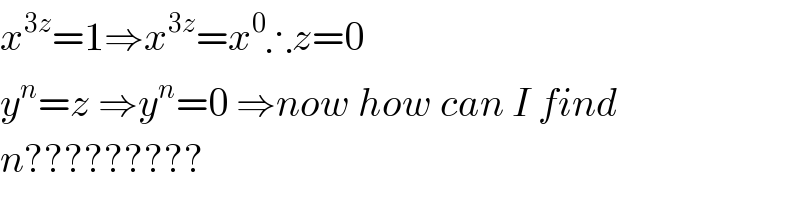
$${x}^{\mathrm{3}{z}} =\mathrm{1}\Rightarrow{x}^{\mathrm{3}{z}} ={x}^{\mathrm{0}} \therefore{z}=\mathrm{0} \\ $$$${y}^{{n}} ={z}\:\Rightarrow{y}^{{n}} =\mathrm{0}\:\Rightarrow{now}\:{how}\:{can}\:{I}\:{find} \\ $$$${n}????????? \\ $$
Commented by Learner last updated on 30/Apr/18
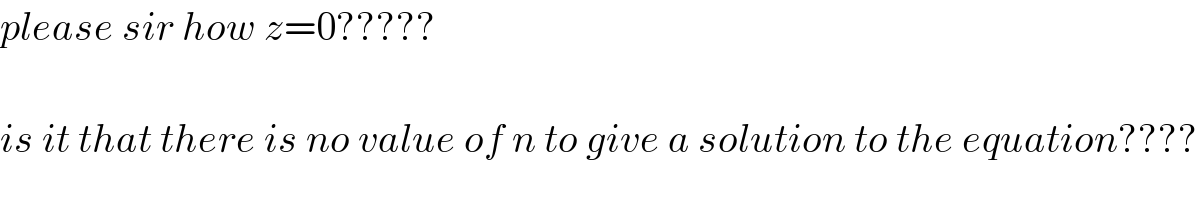
$${please}\:{sir}\:{how}\:{z}=\mathrm{0}????? \\ $$$$ \\ $$$${is}\:{it}\:{that}\:{there}\:{is}\:{no}\:{value}\:{of}\:{n}\:{to}\:{give}\:{a}\:{solution}\:{to}\:{the}\:{equation}???? \\ $$$$ \\ $$
Commented by MJS last updated on 30/Apr/18
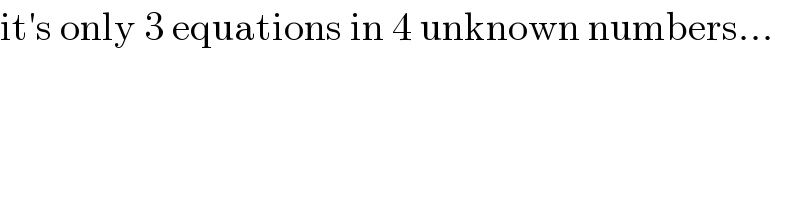
$$\mathrm{it}'\mathrm{s}\:\mathrm{only}\:\mathrm{3}\:\mathrm{equations}\:\mathrm{in}\:\mathrm{4}\:\mathrm{unknown}\:\mathrm{numbers}… \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 30/Apr/18
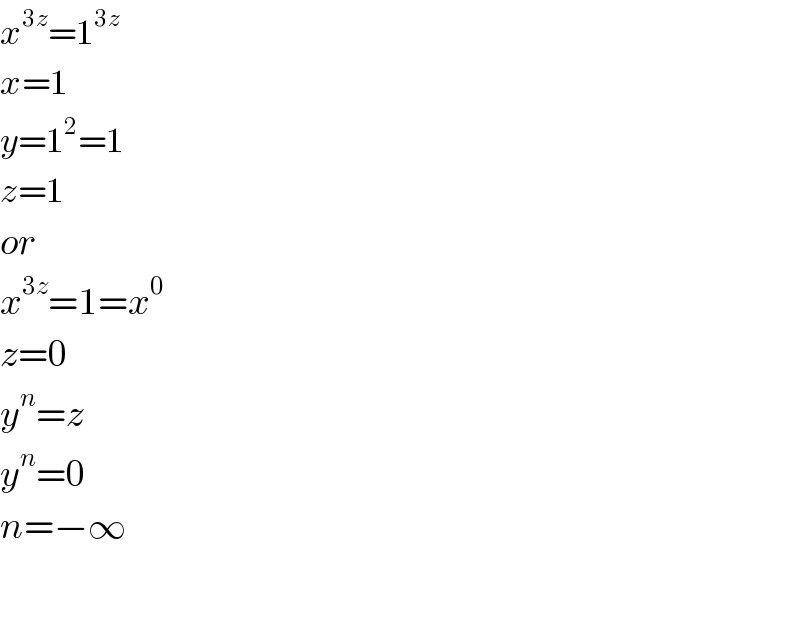
$${x}^{\mathrm{3}{z}} =\mathrm{1}^{\mathrm{3}{z}} \:\:\: \\ $$$${x}=\mathrm{1}\:\:\: \\ $$$${y}=\mathrm{1}^{\mathrm{2}} =\mathrm{1} \\ $$$${z}=\mathrm{1} \\ $$$${or} \\ $$$${x}^{\mathrm{3}{z}} =\mathrm{1}={x}^{\mathrm{0}\:} \\ $$$${z}=\mathrm{0} \\ $$$${y}^{{n}} ={z} \\ $$$${y}^{{n}} =\mathrm{0} \\ $$$${n}=−\infty \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 30/Apr/18
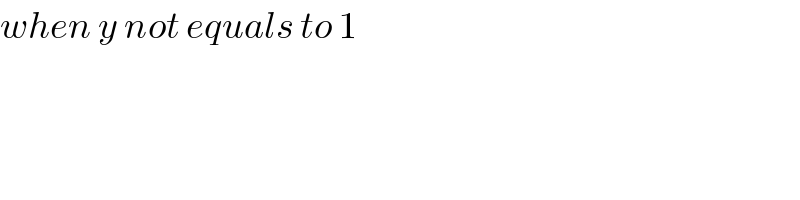
$${when}\:{y}\:{not}\:{equals}\:{to}\:\mathrm{1} \\ $$
Answered by MJS last updated on 30/Apr/18
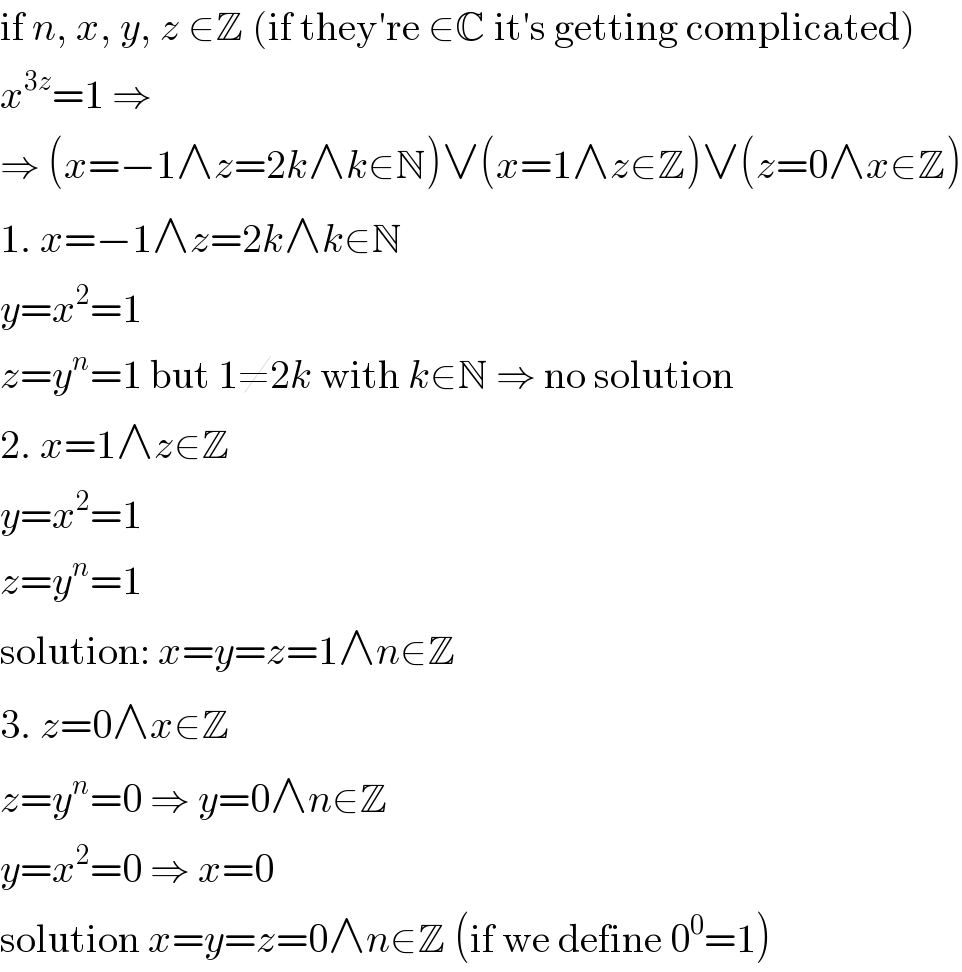
$$\mathrm{if}\:{n},\:{x},\:{y},\:{z}\:\in\mathbb{Z}\:\left(\mathrm{if}\:\mathrm{they}'\mathrm{re}\:\in\mathbb{C}\:\mathrm{it}'\mathrm{s}\:\mathrm{getting}\:\mathrm{complicated}\right) \\ $$$${x}^{\mathrm{3}{z}} =\mathrm{1}\:\Rightarrow \\ $$$$\Rightarrow\:\left({x}=−\mathrm{1}\wedge{z}=\mathrm{2}{k}\wedge{k}\in\mathbb{N}\right)\vee\left({x}=\mathrm{1}\wedge{z}\in\mathbb{Z}\right)\vee\left({z}=\mathrm{0}\wedge{x}\in\mathbb{Z}\right) \\ $$$$\mathrm{1}.\:{x}=−\mathrm{1}\wedge{z}=\mathrm{2}{k}\wedge{k}\in\mathbb{N} \\ $$$${y}={x}^{\mathrm{2}} =\mathrm{1} \\ $$$${z}={y}^{{n}} =\mathrm{1}\:\mathrm{but}\:\mathrm{1}\neq\mathrm{2}{k}\:\mathrm{with}\:{k}\in\mathbb{N}\:\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$$$\mathrm{2}.\:{x}=\mathrm{1}\wedge{z}\in\mathbb{Z} \\ $$$${y}={x}^{\mathrm{2}} =\mathrm{1} \\ $$$${z}={y}^{{n}} =\mathrm{1} \\ $$$$\mathrm{solution}:\:{x}={y}={z}=\mathrm{1}\wedge{n}\in\mathbb{Z} \\ $$$$\mathrm{3}.\:{z}=\mathrm{0}\wedge{x}\in\mathbb{Z} \\ $$$${z}={y}^{{n}} =\mathrm{0}\:\Rightarrow\:{y}=\mathrm{0}\wedge{n}\in\mathbb{Z} \\ $$$${y}={x}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\:{x}=\mathrm{0} \\ $$$$\mathrm{solution}\:{x}={y}={z}=\mathrm{0}\wedge{n}\in\mathbb{Z}\:\left(\mathrm{if}\:\mathrm{we}\:\mathrm{define}\:\mathrm{0}^{\mathrm{0}} =\mathrm{1}\right) \\ $$
Commented by MJS last updated on 30/Apr/18
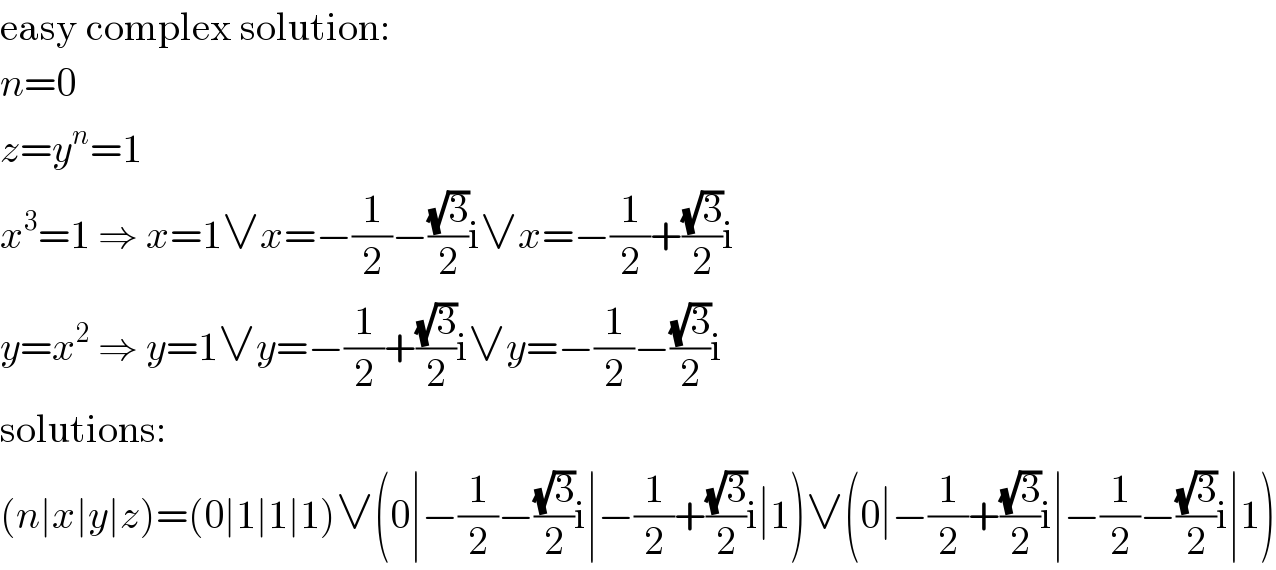
$$\mathrm{easy}\:\mathrm{complex}\:\mathrm{solution}: \\ $$$${n}=\mathrm{0} \\ $$$${z}={y}^{{n}} =\mathrm{1} \\ $$$${x}^{\mathrm{3}} =\mathrm{1}\:\Rightarrow\:{x}=\mathrm{1}\vee{x}=−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\vee{x}=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$$${y}={x}^{\mathrm{2}} \:\Rightarrow\:{y}=\mathrm{1}\vee{y}=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\vee{y}=−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$$$\mathrm{solutions}: \\ $$$$\left({n}\mid{x}\mid{y}\mid{z}\right)=\left(\mathrm{0}\mid\mathrm{1}\mid\mathrm{1}\mid\mathrm{1}\right)\vee\left(\mathrm{0}\mid−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\mid−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\mid\mathrm{1}\right)\vee\left(\mathrm{0}\mid−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\mid−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\mid\mathrm{1}\right) \\ $$
