Question Number 52667 by gunawan last updated on 11/Jan/19
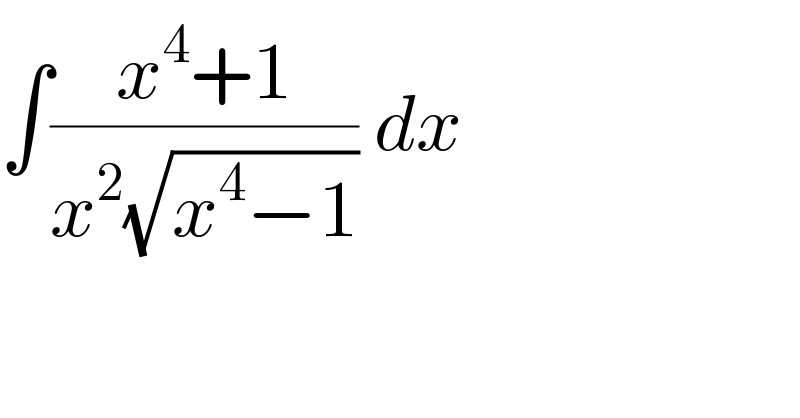
$$\int\frac{{x}^{\mathrm{4}} +\mathrm{1}}{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{4}} −\mathrm{1}}}\:{dx} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 11/Jan/19
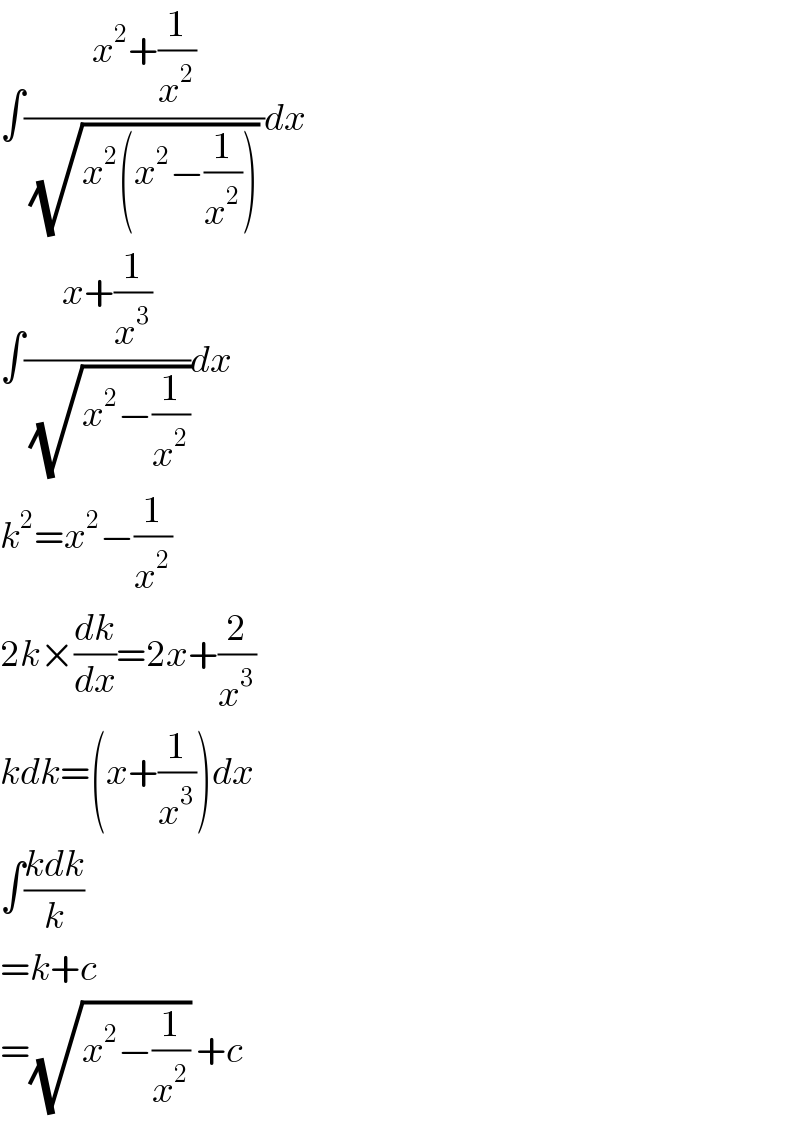
$$\int\frac{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\:\sqrt{{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}\:}{dx} \\ $$$$\int\frac{{x}+\frac{\mathrm{1}}{{x}^{\mathrm{3}} }}{\:\sqrt{{x}^{\mathrm{2}} −\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}{dx} \\ $$$${k}^{\mathrm{2}} ={x}^{\mathrm{2}} −\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$$\mathrm{2}{k}×\frac{{dk}}{{dx}}=\mathrm{2}{x}+\frac{\mathrm{2}}{{x}^{\mathrm{3}} } \\ $$$${kdk}=\left({x}+\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right){dx} \\ $$$$\int\frac{{kdk}}{{k}} \\ $$$$={k}+{c} \\ $$$$=\sqrt{{x}^{\mathrm{2}} −\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\:+{c} \\ $$
Commented by gunawan last updated on 11/Jan/19
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 11/Jan/19

$${most}\:{welcome}… \\ $$
