Question Number 96131 by bemath last updated on 30/May/20
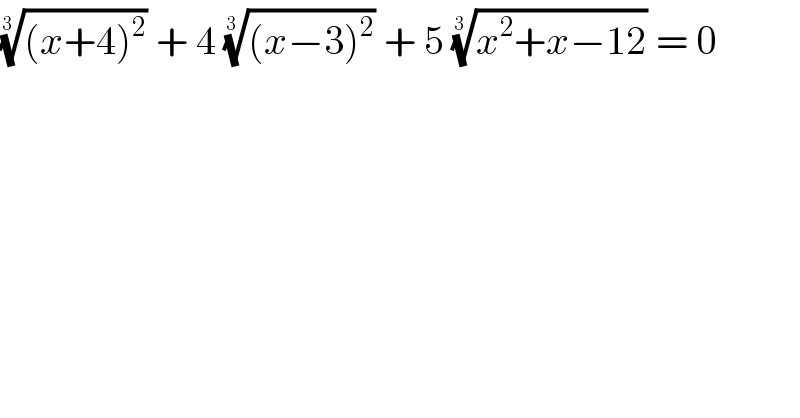
$$\sqrt[{\mathrm{3}\:\:}]{\left({x}+\mathrm{4}\right)^{\mathrm{2}} }\:+\:\mathrm{4}\:\sqrt[{\mathrm{3}\:\:}]{\left({x}−\mathrm{3}\right)^{\mathrm{2}} }\:+\:\mathrm{5}\:\sqrt[{\mathrm{3}\:\:}]{{x}^{\mathrm{2}} +{x}−\mathrm{12}}\:=\:\mathrm{0} \\ $$
Answered by john santu last updated on 30/May/20
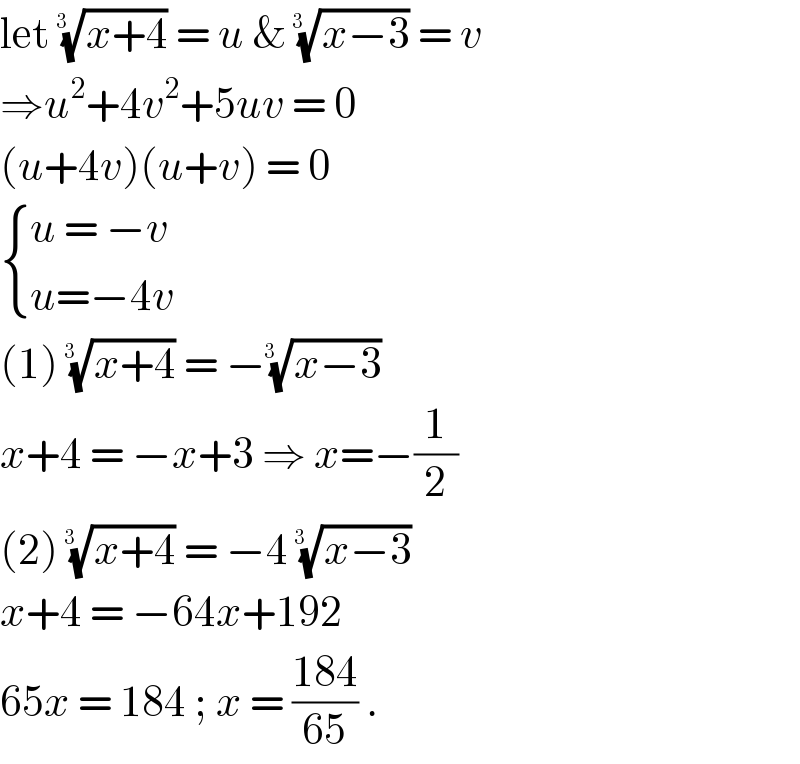
$$\mathrm{let}\:\sqrt[{\mathrm{3}\:\:}]{{x}+\mathrm{4}}\:=\:{u}\:\&\:\sqrt[{\mathrm{3}\:\:}]{{x}−\mathrm{3}}\:=\:{v}\: \\ $$$$\Rightarrow{u}^{\mathrm{2}} +\mathrm{4}{v}^{\mathrm{2}} +\mathrm{5}{uv}\:=\:\mathrm{0} \\ $$$$\left({u}+\mathrm{4}{v}\right)\left({u}+{v}\right)\:=\:\mathrm{0}\: \\ $$$$\begin{cases}{{u}\:=\:−{v}}\\{{u}=−\mathrm{4}{v}}\end{cases} \\ $$$$\left(\mathrm{1}\right)\:\sqrt[{\mathrm{3}\:\:}]{{x}+\mathrm{4}}\:=\:−\sqrt[{\mathrm{3}\:\:}]{{x}−\mathrm{3}} \\ $$$${x}+\mathrm{4}\:=\:−{x}+\mathrm{3}\:\Rightarrow\:{x}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\sqrt[{\mathrm{3}\:\:}]{{x}+\mathrm{4}}\:=\:−\mathrm{4}\:\sqrt[{\mathrm{3}\:\:}]{{x}−\mathrm{3}} \\ $$$${x}+\mathrm{4}\:=\:−\mathrm{64}{x}+\mathrm{192} \\ $$$$\mathrm{65}{x}\:=\:\mathrm{184}\:;\:{x}\:=\:\frac{\mathrm{184}}{\mathrm{65}}\:. \\ $$
