Question Number 121423 by Jamshidbek2311 last updated on 08/Nov/20

$${x}^{\mathrm{4}} −\mathrm{2}\sqrt{\mathrm{2}}{x}^{\mathrm{2}} −{x}+\mathrm{2}−\sqrt{\mathrm{2}}=\mathrm{0}\:\:\:{x}=? \\ $$
Answered by 2004 last updated on 08/Nov/20
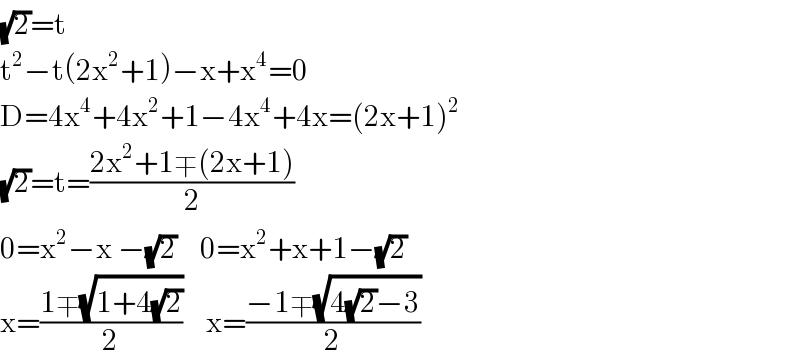
$$\sqrt{\mathrm{2}}=\mathrm{t} \\ $$$$\mathrm{t}^{\mathrm{2}} −\mathrm{t}\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{x}+\mathrm{x}^{\mathrm{4}} =\mathrm{0} \\ $$$$\mathrm{D}=\mathrm{4x}^{\mathrm{4}} +\mathrm{4x}^{\mathrm{2}} +\mathrm{1}−\mathrm{4x}^{\mathrm{4}} +\mathrm{4x}=\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\sqrt{\mathrm{2}}=\mathrm{t}=\frac{\mathrm{2x}^{\mathrm{2}} +\mathrm{1}\mp\left(\mathrm{2x}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\mathrm{0}=\mathrm{x}^{\mathrm{2}} −\mathrm{x}\:−\sqrt{\mathrm{2}}\:\:\:\:\mathrm{0}=\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}−\sqrt{\mathrm{2}} \\ $$$$\mathrm{x}=\frac{\mathrm{1}\mp\sqrt{\mathrm{1}+\mathrm{4}\sqrt{\mathrm{2}}}}{\mathrm{2}}\:\:\:\:\mathrm{x}=\frac{−\mathrm{1}\mp\sqrt{\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{3}}}{\mathrm{2}} \\ $$
Commented by Jamshidbek2311 last updated on 08/Nov/20

$${thank}\:{you} \\ $$
Commented by 2004 last updated on 08/Nov/20

$$\left.\boldsymbol{{Welcome}}\:\boldsymbol{{bro}}\left(\boldsymbol{{arzimaydi}}:\right)\right) \\ $$
Commented by Jamshidbek2311 last updated on 08/Nov/20

$${Are}\:{you}\:{Uzbek}? \\ $$
Commented by pooooop last updated on 10/Nov/20

$$\boldsymbol{{Ha}}.\boldsymbol{{U}}{zbek} \\ $$
Answered by mathmax by abdo last updated on 08/Nov/20

$$\mathrm{e}\Rightarrow\mathrm{x}^{\mathrm{4}} −\sqrt{\mathrm{2}}\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{x}+\mathrm{2}\:=\mathrm{0}\:\:\mathrm{let}\:\sqrt{\mathrm{2}}=\mathrm{t} \\ $$$$\mathrm{e}\Rightarrow\mathrm{x}^{\mathrm{4}} −\mathrm{t}\left(\mathrm{2x}^{\mathrm{2}} \:+\mathrm{1}\right)−\mathrm{x}+\mathrm{t}^{\mathrm{2}} \:=\mathrm{0}\:\Rightarrow\mathrm{t}^{\mathrm{2}} −\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{t}+\mathrm{x}^{\mathrm{4}} −\mathrm{x}\:=\mathrm{0} \\ $$$$\Delta=\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}\right)\:=\mathrm{4x}^{\mathrm{4}} +\mathrm{4x}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{4x}^{\mathrm{4}} \:+\mathrm{4x}=\:\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\sqrt{\mathrm{2}}=\frac{\mathrm{2x}^{\mathrm{2}} +\mathrm{1}+\mathrm{2x}+\mathrm{1}}{\mathrm{2}}\:=\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\:\Rightarrow\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}−\sqrt{\mathrm{2}}=\mathrm{0} \\ $$$$\Delta=\mathrm{1}−\mathrm{4}\left(\mathrm{1}−\sqrt{\mathrm{2}}\right)\:=−\mathrm{3}+\mathrm{4}\sqrt{\mathrm{2}}\:>\mathrm{0}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\frac{−\mathrm{1}+\sqrt{\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =\frac{−\mathrm{1}−\sqrt{\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{3}}}{\mathrm{2}} \\ $$
