Question Number 163222 by cortano1 last updated on 05/Jan/22
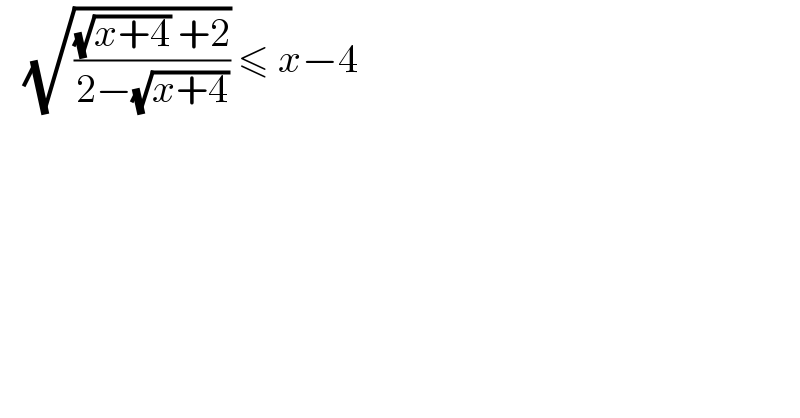
$$\:\:\:\sqrt{\frac{\sqrt{{x}+\mathrm{4}}\:+\mathrm{2}}{\mathrm{2}−\sqrt{{x}+\mathrm{4}}}}\:\leqslant\:{x}−\mathrm{4}\: \\ $$
Answered by blackmamba last updated on 05/Jan/22
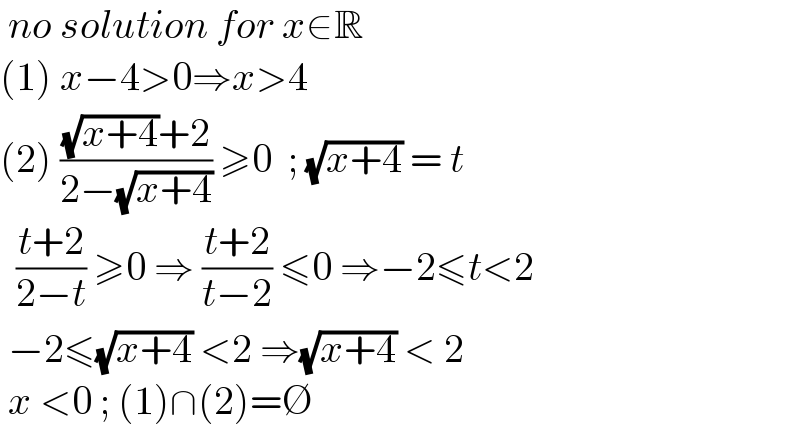
$$\:{no}\:{solution}\:{for}\:{x}\in\mathbb{R} \\ $$$$\left(\mathrm{1}\right)\:{x}−\mathrm{4}>\mathrm{0}\Rightarrow{x}>\mathrm{4} \\ $$$$\left(\mathrm{2}\right)\:\frac{\sqrt{{x}+\mathrm{4}}+\mathrm{2}}{\mathrm{2}−\sqrt{{x}+\mathrm{4}}}\:\geqslant\mathrm{0}\:\:;\:\sqrt{{x}+\mathrm{4}}\:=\:{t} \\ $$$$\:\:\frac{{t}+\mathrm{2}}{\mathrm{2}−{t}}\:\geqslant\mathrm{0}\:\Rightarrow\:\frac{{t}+\mathrm{2}}{{t}−\mathrm{2}}\:\leqslant\mathrm{0}\:\Rightarrow−\mathrm{2}\leqslant{t}<\mathrm{2} \\ $$$$\:−\mathrm{2}\leqslant\sqrt{{x}+\mathrm{4}}\:<\mathrm{2}\:\Rightarrow\sqrt{{x}+\mathrm{4}}\:<\:\mathrm{2}\: \\ $$$$\:{x}\:<\mathrm{0}\:;\:\left(\mathrm{1}\right)\cap\left(\mathrm{2}\right)=\varnothing\: \\ $$
