Menu Close

x-4-3x-2-2x-1-x-1-

Tinku Tara 0 Comments
Pin




Question Number 60854 by Askash last updated on 26/May/19
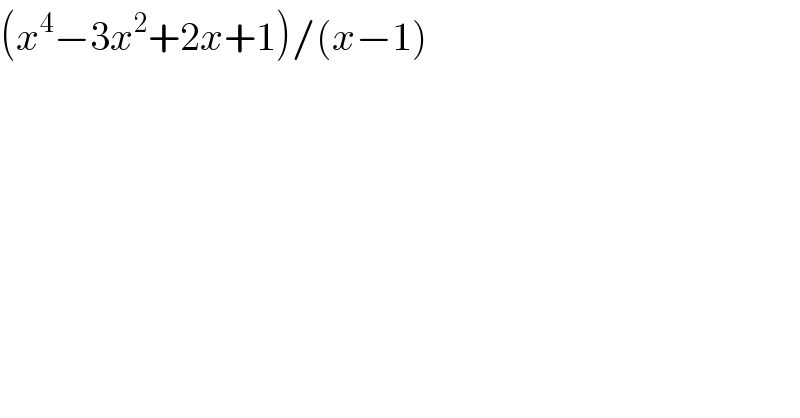
(x^4 −3x^2 +2x+1)/(x−1)
$$\left({x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}\right)/\left({x}−\mathrm{1}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by Askash last updated on 26/May/19
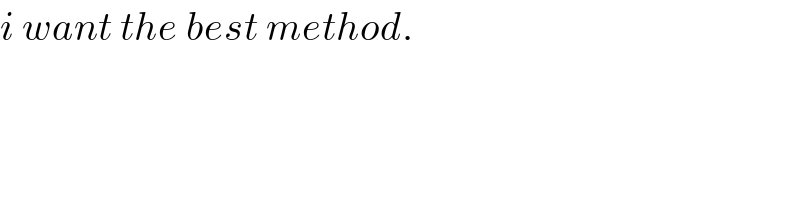
i want the best method.
$${i}\:{want}\:{the}\:{best}\:{method}. \\ $$
Commented by maxmathsup by imad last updated on 26/May/19
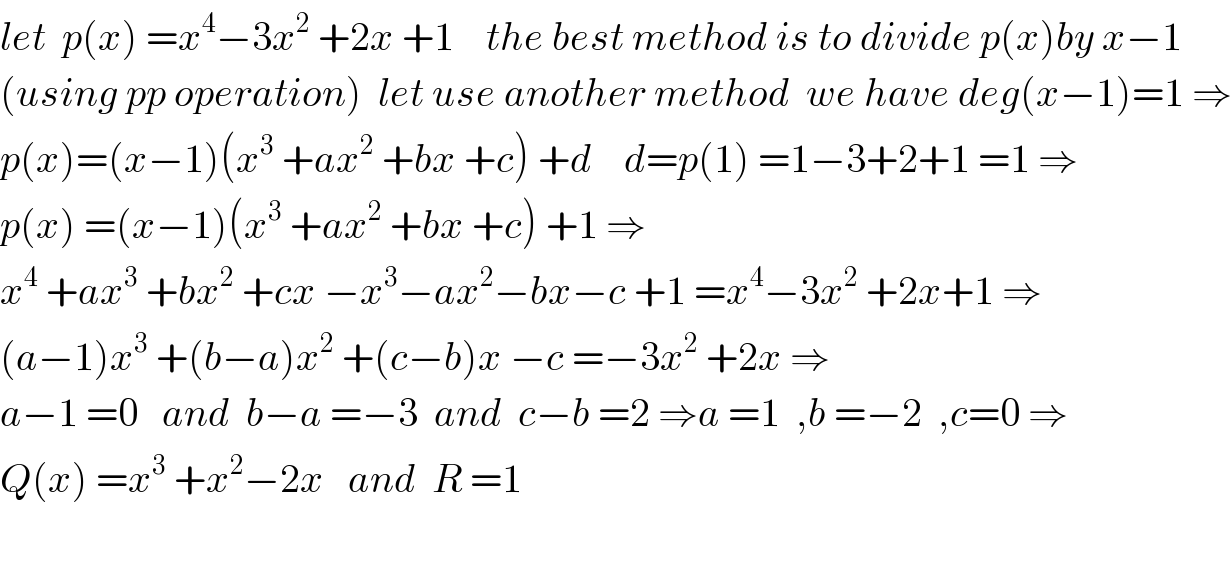
let p(x) =x^4 −3x^2 +2x +1 the best method is to divide p(x)by x−1 (using pp operation) let use another method we have deg(x−1)=1 ⇒ p(x)=(x−1)(x^3 +ax^2 +bx +c) +d d=p(1) =1−3+2+1 =1 ⇒ p(x) =(x−1)(x^3 +ax^2 +bx +c) +1 ⇒ x^4 +ax^3 +bx^2 +cx −x^3 −ax^2 −bx−c +1 =x^4 −3x^2 +2x+1 ⇒ (a−1)x^3 +(b−a)x^2 +(c−b)x −c =−3x^2 +2x ⇒ a−1 =0 and b−a =−3 and c−b =2 ⇒a =1 ,b =−2 ,c=0 ⇒ Q(x) =x^3 +x^2 −2x and R =1
$${let}\:\:{p}\left({x}\right)\:={x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{2}} \:+\mathrm{2}{x}\:+\mathrm{1}\:\:\:\:{the}\:{best}\:{method}\:{is}\:{to}\:{divide}\:{p}\left({x}\right){by}\:{x}−\mathrm{1} \\ $$$$\left({using}\:{pp}\:{operation}\right)\:\:{let}\:{use}\:{another}\:{method}\:\:{we}\:{have}\:{deg}\left({x}−\mathrm{1}\right)=\mathrm{1}\:\Rightarrow \\ $$$${p}\left({x}\right)=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{3}} \:+{ax}^{\mathrm{2}} \:+{bx}\:+{c}\right)\:+{d}\:\:\:\:{d}={p}\left(\mathrm{1}\right)\:=\mathrm{1}−\mathrm{3}+\mathrm{2}+\mathrm{1}\:=\mathrm{1}\:\Rightarrow \\ $$$${p}\left({x}\right)\:=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{3}} \:+{ax}^{\mathrm{2}} \:+{bx}\:+{c}\right)\:+\mathrm{1}\:\Rightarrow \\ $$$${x}^{\mathrm{4}} \:+{ax}^{\mathrm{3}} \:+{bx}^{\mathrm{2}} \:+{cx}\:−{x}^{\mathrm{3}} −{ax}^{\mathrm{2}} −{bx}−{c}\:+\mathrm{1}\:={x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{1}\:\Rightarrow \\ $$$$\left({a}−\mathrm{1}\right){x}^{\mathrm{3}} \:+\left({b}−{a}\right){x}^{\mathrm{2}} \:+\left({c}−{b}\right){x}\:−{c}\:=−\mathrm{3}{x}^{\mathrm{2}} \:+\mathrm{2}{x}\:\Rightarrow \\ $$$${a}−\mathrm{1}\:=\mathrm{0}\:\:\:{and}\:\:{b}−{a}\:=−\mathrm{3}\:\:{and}\:\:{c}−{b}\:=\mathrm{2}\:\Rightarrow{a}\:=\mathrm{1}\:\:,{b}\:=−\mathrm{2}\:\:,{c}=\mathrm{0}\:\Rightarrow \\ $$$${Q}\left({x}\right)\:={x}^{\mathrm{3}} \:+{x}^{\mathrm{2}} −\mathrm{2}{x}\:\:\:{and}\:\:{R}\:=\mathrm{1} \\ $$$$ \\ $$
Commented by Tawa1 last updated on 26/May/19
let x − 1 = 0, ⇒ x = 1 So, by remainder theorem f(x) = x^4 − 3x^2 + 2x + 1 f(1) = 1^4 − 3(1)^2 + 2(1) + 1 f(1) = 1 − 3 + 2 + 1 f(1) = 1 So, the remainder is 1.
$$\:\:\:\mathrm{let}\:\:\:\:\mathrm{x}\:−\:\mathrm{1}\:\:=\:\:\mathrm{0},\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:\mathrm{x}\:=\:\mathrm{1}\:\:\:\: \\ $$$$\mathrm{So},\:\mathrm{by}\:\mathrm{remainder}\:\mathrm{theorem} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)\:\:=\:\:\mathrm{x}^{\mathrm{4}} \:−\:\mathrm{3x}^{\mathrm{2}} \:+\:\mathrm{2x}\:+\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{f}\left(\mathrm{1}\right)\:\:=\:\:\mathrm{1}^{\mathrm{4}} \:−\:\mathrm{3}\left(\mathrm{1}\right)^{\mathrm{2}} \:+\:\mathrm{2}\left(\mathrm{1}\right)\:+\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{f}\left(\mathrm{1}\right)\:\:=\:\:\mathrm{1}\:−\:\mathrm{3}\:+\:\mathrm{2}\:+\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{f}\left(\mathrm{1}\right)\:\:=\:\:\mathrm{1} \\ $$$$\mathrm{So},\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{is}\:\mathrm{1}. \\ $$
Commented by Askash last updated on 26/May/19
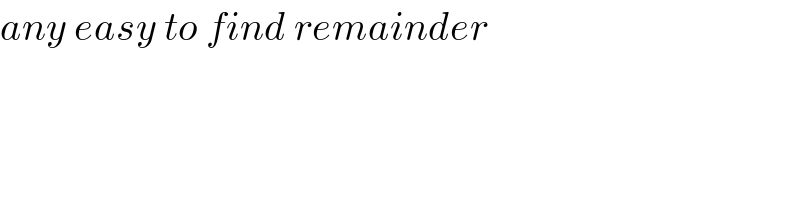
any easy to find remainder
$${any}\:{easy}\:{to}\:{find}\:{remainder} \\ $$
Answered by ajfour last updated on 26/May/19
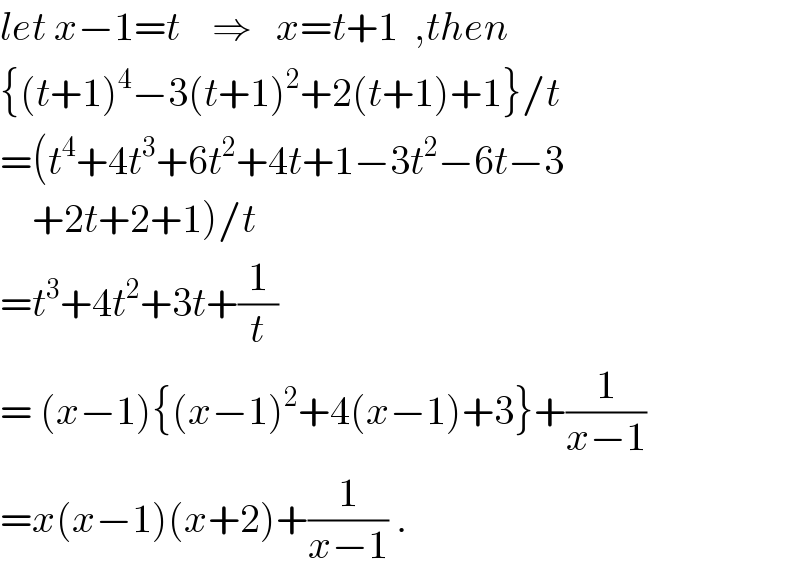
let x−1=t ⇒ x=t+1 ,then {(t+1)^4 −3(t+1)^2 +2(t+1)+1}/t =(t^4 +4t^3 +6t^2 +4t+1−3t^2 −6t−3 +2t+2+1)/t =t^3 +4t^2 +3t+(1/t) = (x−1){(x−1)^2 +4(x−1)+3}+(1/(x−1)) =x(x−1)(x+2)+(1/(x−1)) .
$${let}\:{x}−\mathrm{1}={t}\:\:\:\:\Rightarrow\:\:\:{x}={t}+\mathrm{1}\:\:,{then} \\ $$$$\left\{\left({t}+\mathrm{1}\right)^{\mathrm{4}} −\mathrm{3}\left({t}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}\left({t}+\mathrm{1}\right)+\mathrm{1}\right\}/{t} \\ $$$$=\left({t}^{\mathrm{4}} +\mathrm{4}{t}^{\mathrm{3}} +\mathrm{6}{t}^{\mathrm{2}} +\mathrm{4}{t}+\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} −\mathrm{6}{t}−\mathrm{3}\right. \\ $$$$\left.\:\:\:\:+\mathrm{2}{t}+\mathrm{2}+\mathrm{1}\right)/{t} \\ $$$$={t}^{\mathrm{3}} +\mathrm{4}{t}^{\mathrm{2}} +\mathrm{3}{t}+\frac{\mathrm{1}}{{t}} \\ $$$$=\:\left({x}−\mathrm{1}\right)\left\{\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}\left({x}−\mathrm{1}\right)+\mathrm{3}\right\}+\frac{\mathrm{1}}{{x}−\mathrm{1}} \\ $$$$={x}\left({x}−\mathrm{1}\right)\left({x}+\mathrm{2}\right)+\frac{\mathrm{1}}{{x}−\mathrm{1}}\:. \\ $$
Answered by Rasheed.Sindhi last updated on 26/May/19
Synthetic Division is perhaps the easiest way when divisor is linear as in this case. P(x)=x^4 +0x^3 −3x^2 +2x+1 D(x)=x−1 Q(x):Quotient∫ R: Remainder (((1)),1,0,(−3),( 2),1),(,,1,( 1),(−2),0),(,−,−,−,−,−),(,1,1,(−2),( 0),([1)) ) Q(x)=x^3 +x^2 −2x , R=1
$${Synthetic}\:{Division}\:{is}\:{perhaps}\:{the} \\ $$$${easiest}\:{way}\:{when}\:\:{divisor}\:{is}\:{linear} \\ $$$${as}\:{in}\:{this}\:{case}. \\ $$$${P}\left({x}\right)={x}^{\mathrm{4}} +\mathrm{0}{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1} \\ $$$${D}\left({x}\right)={x}−\mathrm{1} \\ $$$${Q}\left({x}\right):{Quotient}\int \\ $$$${R}:\:{Remainder} \\ $$$$\begin{pmatrix}{\left.\mathrm{1}\right)}&{\mathrm{1}}&{\mathrm{0}}&{−\mathrm{3}}&{\:\:\:\:\mathrm{2}}&{\mathrm{1}}\\{}&{}&{\mathrm{1}}&{\:\:\:\:\mathrm{1}}&{−\mathrm{2}}&{\mathrm{0}}\\{}&{−}&{−}&{−}&{−}&{−}\\{}&{\mathrm{1}}&{\mathrm{1}}&{−\mathrm{2}}&{\:\:\:\:\:\mathrm{0}}&{\left[\mathrm{1}\right.}\end{pmatrix} \\ $$$${Q}\left({x}\right)={x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{2}{x}\:,\:\:{R}=\mathrm{1} \\ $$
Commented by malwaan last updated on 26/May/19
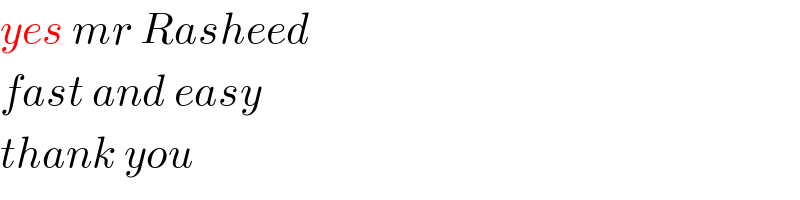
yes mr Rasheed fast and easy thank you
$${yes}\:{mr}\:{Rasheed} \\ $$$${fast}\:{and}\:{easy} \\ $$$${thank}\:{you} \\ $$
Commented by Rasheed.Sindhi last updated on 27/May/19
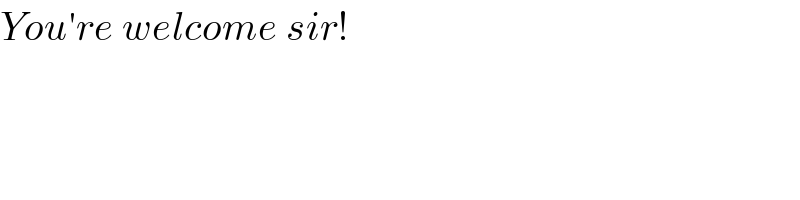
You′re welcome sir!
$${You}'{re}\:{welcome}\:{sir}! \\ $$
Commented by Rasheed.Sindhi last updated on 27/May/19
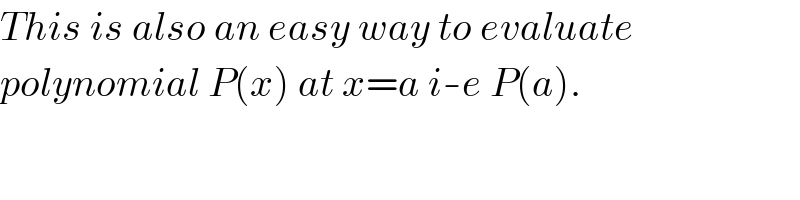
This is also an easy way to evaluate polynomial P(x) at x=a i-e P(a).
$${This}\:{is}\:{also}\:{an}\:{easy}\:{way}\:{to}\:{evaluate} \\ $$$${polynomial}\:{P}\left({x}\right)\:{at}\:{x}={a}\:{i}-{e}\:{P}\left({a}\right). \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *