Menu Close

x-4-4x-2-x-2-4-dx-

Tinku Tara 0 Comments
Pin




Question Number 93638 by i jagooll last updated on 14/May/20
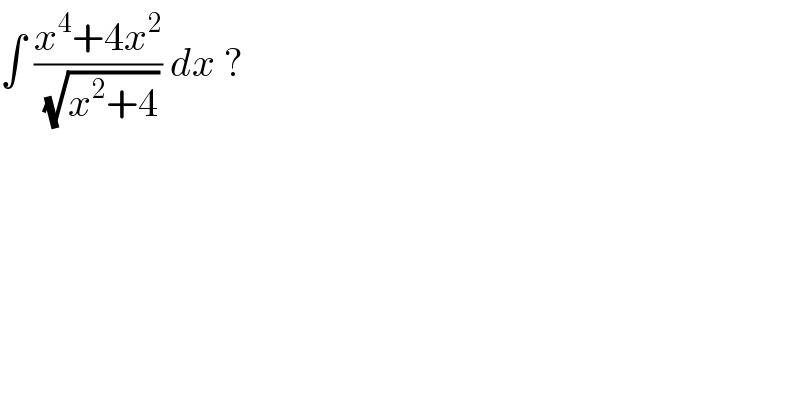
∫ ((x^4 +4x^2 )/( (√(x^2 +4)))) dx ?
$$\int\:\frac{{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}}\:{dx}\:?\: \\ $$
Commented by i jagooll last updated on 14/May/20
thank you both
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{both}\: \\ $$
Commented by mathmax by abdo last updated on 14/May/20
I =∫ ((x^4 +4x^2 )/( (√(x^2 +4))))dx changement (√(x^2 +4))=t give x^2 =t^2 −4 ⇒xdx =tdt I =∫ (((t^2 −4)^3 +4(√(t^2 −4)))/t)tdt =∫( (t^2 −4)^3 +4(√(t^2 −4)))dt =∫ (t^2 −4)^3 dt +4 ∫(√(t^2 −4))dt but ∫ (t^2 −4)^3 dt =∫ (t^6 −3t^4 (4)+3t^2 (4)^2 −4^3 )dt =(t^7 /7) −((12)/5)t^5 +((48)/3) t^3 −64 t +c_1 ∫ (√(t^2 −4))dt =_(t =2chz) ∫ 2 shz (2shz)dz =4 ∫ sh^2 z dz =2∫ (ch(2z)−1)dz =sh(2z)−2z +c_2 =2sh(z)ch(z) −2z +c_2 =2(√(ch^2 z−1))×(t/2) −2argch((t/2)) +c_2 =t(√((t^2 /4)−1)) −2 ln((t/2)+(√((t^2 /4)−1))) +c_2 ⇒ I =(1/7)((√(x^2 +4)))^7 −((12)/5)((√(x^2 +4)))^5 +16((√(x^2 +4)))^3 −64(√(x^2 +4)) +2t(√(t^2 −4)) −2ln(t+(√(t^2 −4))) +C
$${I}\:=\int\:\:\frac{{x}^{\mathrm{4}} \:+\mathrm{4}{x}^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}}}{dx}\:\:{changement}\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}}={t}\:{give}\:{x}^{\mathrm{2}} \:={t}^{\mathrm{2}} −\mathrm{4}\:\Rightarrow{xdx}\:={tdt} \\ $$$${I}\:=\int\:\:\frac{\left({t}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{3}} \:+\mathrm{4}\sqrt{{t}^{\mathrm{2}} −\mathrm{4}}}{{t}}{tdt}\:=\int\left(\:\left({t}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{3}} \:+\mathrm{4}\sqrt{{t}^{\mathrm{2}} −\mathrm{4}}\right){dt} \\ $$$$=\int\:\left({t}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{3}} \:{dt}\:+\mathrm{4}\:\int\sqrt{{t}^{\mathrm{2}} −\mathrm{4}}{dt}\:\:{but} \\ $$$$\int\:\left({t}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{3}} \:{dt}\:=\int\:\:\left({t}^{\mathrm{6}} −\mathrm{3}{t}^{\mathrm{4}} \left(\mathrm{4}\right)+\mathrm{3}{t}^{\mathrm{2}} \left(\mathrm{4}\right)^{\mathrm{2}} −\mathrm{4}^{\mathrm{3}} \right){dt} \\ $$$$=\frac{{t}^{\mathrm{7}} }{\mathrm{7}}\:−\frac{\mathrm{12}}{\mathrm{5}}{t}^{\mathrm{5}} \:+\frac{\mathrm{48}}{\mathrm{3}}\:{t}^{\mathrm{3}} \:−\mathrm{64}\:{t}\:+{c}_{\mathrm{1}} \\ $$$$\int\:\sqrt{{t}^{\mathrm{2}} −\mathrm{4}}{dt}\:\:=_{{t}\:=\mathrm{2}{chz}} \:\:\int\:\mathrm{2}\:{shz}\:\left(\mathrm{2}{shz}\right){dz}\:=\mathrm{4}\:\int\:{sh}^{\mathrm{2}} {z}\:{dz} \\ $$$$=\mathrm{2}\int\:\left({ch}\left(\mathrm{2}{z}\right)−\mathrm{1}\right){dz}\:={sh}\left(\mathrm{2}{z}\right)−\mathrm{2}{z}\:+{c}_{\mathrm{2}} \\ $$$$=\mathrm{2}{sh}\left({z}\right){ch}\left({z}\right)\:−\mathrm{2}{z}\:+{c}_{\mathrm{2}} \\ $$$$=\mathrm{2}\sqrt{{ch}^{\mathrm{2}} {z}−\mathrm{1}}×\frac{{t}}{\mathrm{2}}\:−\mathrm{2}{argch}\left(\frac{{t}}{\mathrm{2}}\right)\:+{c}_{\mathrm{2}} \\ $$$$={t}\sqrt{\frac{{t}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{1}}\:−\mathrm{2}\:{ln}\left(\frac{{t}}{\mathrm{2}}+\sqrt{\frac{{t}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{1}}\right)\:+{c}_{\mathrm{2}} \Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{7}}\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}\right)^{\mathrm{7}} −\frac{\mathrm{12}}{\mathrm{5}}\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}\right)^{\mathrm{5}} \:+\mathrm{16}\left(\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}}\right)^{\mathrm{3}} −\mathrm{64}\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}} \\ $$$$+\mathrm{2}{t}\sqrt{{t}^{\mathrm{2}} −\mathrm{4}}\:\:−\mathrm{2}{ln}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{4}}\right)\:+{C} \\ $$$$ \\ $$
Answered by Ar Brandon last updated on 14/May/20
L=∫ ((x^4 +4x^2 )/( (√(x^2 +4)))) dx=∫x^2 ∙((x^2 +4)/( (√(x^2 +4))))dx=∫x^2 (√(x^2 +4))dx x=2sinhθ⇒dx=2coshθdθ L=∫4sinh^2 θ∙(√(4sinh^2 θ+4))∙2coshθdθ ⇒L=4∫4sinh^2 θcosh^2 θdθ=4∫sinh^2 2θdθ ⇒L=2∫(cosh4θ−1)=((sinh4θ)/2)−2θ+C ∫ ((x^4 +4x^2 )/( (√(x^2 +4)))) dx =(1/2)sinh4sinh^(−1) ((x/2))−2sinh^(−1) ((x/2))+C
$$\mathrm{L}=\int\:\frac{{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}}\:\mathrm{d}{x}=\int{x}^{\mathrm{2}} \centerdot\frac{{x}^{\mathrm{2}} +\mathrm{4}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}}\mathrm{d}{x}=\int{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +\mathrm{4}}\mathrm{d}{x}\: \\ $$$${x}=\mathrm{2sinh}\theta\Rightarrow\mathrm{d}{x}=\mathrm{2cosh}\theta\mathrm{d}\theta \\ $$$$\mathrm{L}=\int\mathrm{4sinh}^{\mathrm{2}} \theta\centerdot\sqrt{\mathrm{4sinh}^{\mathrm{2}} \theta+\mathrm{4}}\centerdot\mathrm{2cosh}\theta\mathrm{d}\theta \\ $$$$\Rightarrow\mathrm{L}=\mathrm{4}\int\mathrm{4sinh}^{\mathrm{2}} \theta\mathrm{cosh}^{\mathrm{2}} \theta\mathrm{d}\theta=\mathrm{4}\int\mathrm{sinh}^{\mathrm{2}} \mathrm{2}\theta\mathrm{d}\theta \\ $$$$\Rightarrow\mathrm{L}=\mathrm{2}\int\left(\mathrm{cosh4}\theta−\mathrm{1}\right)=\frac{\mathrm{sinh4}\theta}{\mathrm{2}}−\mathrm{2}\theta+\mathrm{C} \\ $$$$\int\:\frac{{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}}\:{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinh4sinh}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{2sinh}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{2}}\right)+\mathrm{C} \\ $$
Answered by Kunal12588 last updated on 14/May/20
I=∫((x^2 (x^2 +4))/( (√(x^2 +4))))dx x^2 +4=t ⇒dx=(1/(2(√(t−4))))dt I=(1/2)∫(((t−4)t)/( (√t)(√(t−4))))dt=(1/2)∫(√t)(√(t−4)) dt=(1/2)∫(√(t^2 −4t)) dt =(1/2)∫(√((t−2)^2 −4)) dt =(1/2)[(1/2)(t−2)(√(t^2 −4t))−(4/2)ln∣t−2+(√(t^2 −4t))∣]+C =(1/2)[(1/2)x(x^2 +2)(√(x^2 +4))−2ln∣x^2 +2+x(√(x^2 +4))∣]+C =(1/4)x(x^2 +2)(√(x^2 +4))−ln∣x^2 +x(√(x^2 +4))+2∣+C
$${I}=\int\frac{{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{4}\right)}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}}{dx} \\ $$$${x}^{\mathrm{2}} +\mathrm{4}={t} \\ $$$$\Rightarrow{dx}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{t}−\mathrm{4}}}{dt} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left({t}−\mathrm{4}\right){t}}{\:\sqrt{{t}}\sqrt{{t}−\mathrm{4}}}{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int\sqrt{{t}}\sqrt{{t}−\mathrm{4}}\:{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int\sqrt{{t}^{\mathrm{2}} −\mathrm{4}{t}}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\sqrt{\left({t}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{4}}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{2}}\left({t}−\mathrm{2}\right)\sqrt{{t}^{\mathrm{2}} −\mathrm{4}{t}}−\frac{\mathrm{4}}{\mathrm{2}}{ln}\mid{t}−\mathrm{2}+\sqrt{{t}^{\mathrm{2}} −\mathrm{4}{t}}\mid\right]+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{2}}{x}\left({x}^{\mathrm{2}} +\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}−\mathrm{2}{ln}\mid{x}^{\mathrm{2}} +\mathrm{2}+{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}\mid\right]+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{x}\left({x}^{\mathrm{2}} +\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}−{ln}\mid{x}^{\mathrm{2}} +{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}+\mathrm{2}\mid+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *