x-4-5x-2-4-0-

Question Number 117620 by Dwaipayan Shikari last updated on 12/Oct/20

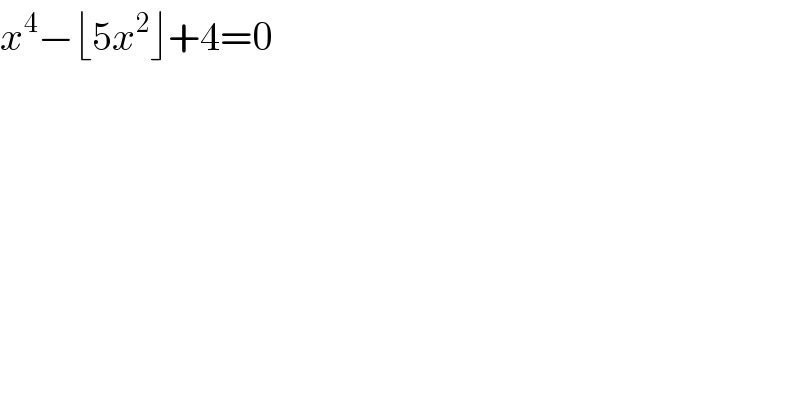
$${x}^{\mathrm{4}} −\lfloor\mathrm{5}{x}^{\mathrm{2}} \rfloor+\mathrm{4}=\mathrm{0} \\ $$

Answered by mr W last updated on 12/Oct/20

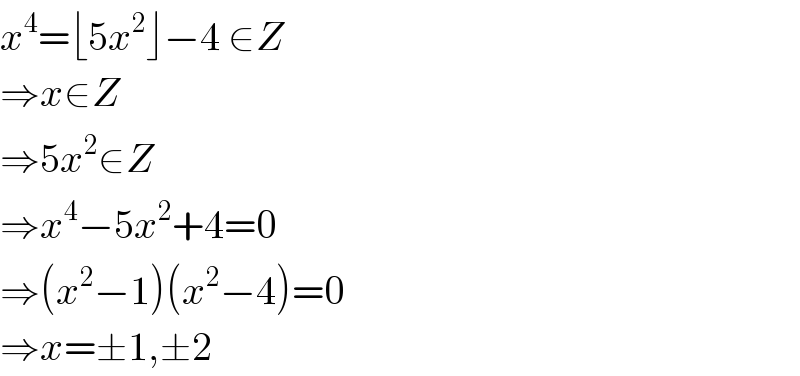
x^4 =⌊5x^2 ⌋−4 ∈Z ⇒x∈Z ⇒5x^2 ∈Z ⇒x^4 −5x^2 +4=0 ⇒(x^2 −1)(x^2 −4)=0 ⇒x=±1,±2

$${x}^{\mathrm{4}} =\lfloor\mathrm{5}{x}^{\mathrm{2}} \rfloor−\mathrm{4}\:\in{Z} \\ $$$$\Rightarrow{x}\in{Z} \\ $$$$\Rightarrow\mathrm{5}{x}^{\mathrm{2}} \in{Z} \\ $$$$\Rightarrow{x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{4}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=\pm\mathrm{1},\pm\mathrm{2} \\ $$

Commented by floor(10²Eta[1]) last updated on 12/Oct/20

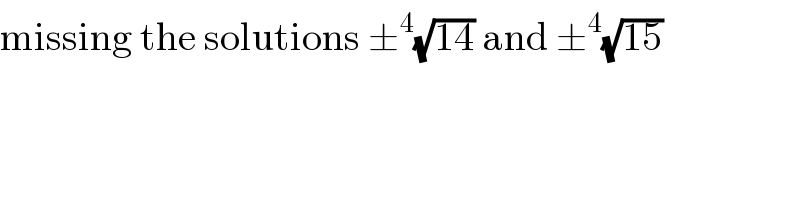
missing the solutions ±^4 (√(14)) and ±^4 (√(15))

$$\mathrm{missing}\:\mathrm{the}\:\mathrm{solutions}\:\pm^{\mathrm{4}} \sqrt{\mathrm{14}}\:\mathrm{and}\:\pm^{\mathrm{4}} \sqrt{\mathrm{15}} \\ $$

Commented by mr W last updated on 13/Oct/20

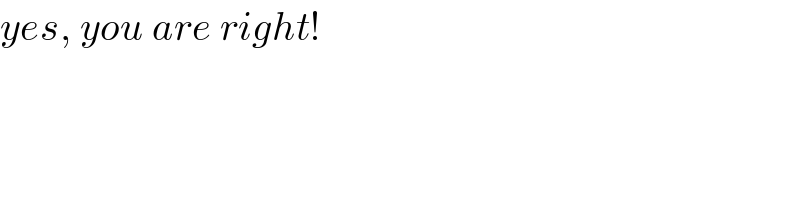
$${yes},\:{you}\:{are}\:{right}! \\ $$

Answered by AbduraufKodiriy last updated on 12/Oct/20

x^2 =t t^2 −⌊5t⌋+4=0 ⌊5t⌋=t^2 +4 ∈ Z {5t}=−(t^2 −5t+4) 0≤−(t^2 −5t+4)<1 ⇒ t∈[1; ((5−(√5))/2))∪(((5+(√5))/2); 4] Thus, (t^2 +4)∈[5; ((23−5(√5))/2))∪(((23+5(√5))/2); 20] approximately: (t^2 +4)∈[5; 5.9)∪(17.09; 20] So, 1) t^2 +4=5 ⇒ t=1 2) t^2 +4=18 ⇒ t=(√(14)); 3) t^2 +4=19 ⇒ t=(√(15)); 4) t^2 +4=20 ⇒ t=4 Answer: x_(1,2) =±1, x_(3,4) =±((14))^(1/4) , x_(5,6) =±((15))^(1/4) , x_(7,8) =±2

$$\boldsymbol{{x}}^{\mathrm{2}} =\boldsymbol{{t}} \\ $$$$\boldsymbol{{t}}^{\mathrm{2}} −\lfloor\mathrm{5}\boldsymbol{{t}}\rfloor+\mathrm{4}=\mathrm{0} \\ $$$$\lfloor\mathrm{5}\boldsymbol{{t}}\rfloor=\boldsymbol{{t}}^{\mathrm{2}} +\mathrm{4}\:\in\:\boldsymbol{{Z}} \\ $$$$\left\{\mathrm{5}\boldsymbol{{t}}\right\}=−\left(\boldsymbol{{t}}^{\mathrm{2}} −\mathrm{5}\boldsymbol{{t}}+\mathrm{4}\right) \\ $$$$\mathrm{0}\leqslant−\left(\boldsymbol{{t}}^{\mathrm{2}} −\mathrm{5}\boldsymbol{{t}}+\mathrm{4}\right)<\mathrm{1}\:\Rightarrow\:\boldsymbol{{t}}\in\left[\mathrm{1};\:\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\cup\left(\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{2}};\:\mathrm{4}\right] \\ $$$$\boldsymbol{{Thus}},\:\left(\boldsymbol{{t}}^{\mathrm{2}} +\mathrm{4}\right)\in\left[\mathrm{5};\:\frac{\mathrm{23}−\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\cup\left(\frac{\mathrm{23}+\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{2}};\:\mathrm{20}\right] \\ $$$$\boldsymbol{{approximately}}:\:\left(\boldsymbol{{t}}^{\mathrm{2}} +\mathrm{4}\right)\in\left[\mathrm{5};\:\mathrm{5}.\mathrm{9}\right)\cup\left(\mathrm{17}.\mathrm{09};\:\mathrm{20}\right] \\ $$$$\left.\boldsymbol{{S}}\left.\boldsymbol{{o}},\:\mathrm{1}\right)\:\boldsymbol{{t}}^{\mathrm{2}} +\mathrm{4}=\mathrm{5}\:\Rightarrow\:\boldsymbol{{t}}=\mathrm{1}\:\:\:\:\:\:\mathrm{2}\right)\:\boldsymbol{{t}}^{\mathrm{2}} +\mathrm{4}=\mathrm{18}\:\Rightarrow\:\boldsymbol{{t}}=\sqrt{\mathrm{14}}; \\ $$$$\left.\mathrm{3}\left.\right)\:\boldsymbol{{t}}^{\mathrm{2}} +\mathrm{4}=\mathrm{19}\:\Rightarrow\:\boldsymbol{{t}}=\sqrt{\mathrm{15}};\:\:\:\:\:\:\:\:\:\mathrm{4}\right)\:\boldsymbol{{t}}^{\mathrm{2}} +\mathrm{4}=\mathrm{20}\:\Rightarrow\:\boldsymbol{{t}}=\mathrm{4} \\ $$$$\boldsymbol{{Answer}}:\:\boldsymbol{{x}}_{\mathrm{1},\mathrm{2}} =\pm\mathrm{1},\:\boldsymbol{{x}}_{\mathrm{3},\mathrm{4}} =\pm\sqrt[{\mathrm{4}}]{\mathrm{14}},\:\boldsymbol{{x}}_{\mathrm{5},\mathrm{6}} =\pm\sqrt[{\mathrm{4}}]{\mathrm{15}},\:\boldsymbol{{x}}_{\mathrm{7},\mathrm{8}} =\pm\mathrm{2} \\ $$

Answered by floor(10²Eta[1]) last updated on 12/Oct/20

x^4 −⌊5x^2 ⌋=−4∈Z but ⌊5x^2 ⌋∈Z⇒x^4 ∈N ⇒x∈Z or x=±^4 (√a), a∈N ⌊5x^2 ⌋=n⇒5x^2 =n+θ, n∈Z, 0≤θ<1 x^2 =((n+θ)/5) x^4 =((n^2 +2nθ+θ^2 )/(25)) ((n^2 +2nθ+θ^2 )/(25))−n+4=0 n^2 +(2θ−25)n+100+θ^2 =0 n=((25−2θ±(√(225−100θ)))/2)∈Z since 0≤θ<1 so: I case: 15≥(√(225−100θ))>11 ⇒40≥40−2θ≥25−2θ+(√(225−100θ))>36−2θ>34 ⇒20≥n>17∴n∈{18,19,20} II case: 8<10−2θ≤25−2θ−(√(225−100θ))<14−2θ≤14 4<n<7⇒n∈{5,6} ⇒n=5 x^2 =((5+θ)/5)=1+(θ/5)⇒1≤x^2 <(6/5)=1.2 x=±1 ⇒n=6(no sol.) ⇒n=18 x^2 =((18+θ)/5)⇒3.6≤x^2 <3.8⇒x∉N x^2 =(√a), a∈N⇒3.6^2 ≤a<3.8^2 ⇒a∈{13,14} ⇒x=±^4 (√(14)) ⇒n=19 x^2 =((19+θ)/5)⇒3.8≤x^2 <4⇒x∉N x^2 =(√a) ⇒3.8^2 ≤a<16⇒a=15 ⇒x=±^4 (√(15)) n=20 x^2 =((20+θ)/5)⇒4≤x^2 <5⇒x=±2 all the solutions are: x={±1, ±^4 (√(14)), ±^4 (√(15)), ±2}

$$\mathrm{x}^{\mathrm{4}} −\lfloor\mathrm{5x}^{\mathrm{2}} \rfloor=−\mathrm{4}\in\mathbb{Z} \\ $$$$\mathrm{but}\:\lfloor\mathrm{5x}^{\mathrm{2}} \rfloor\in\mathbb{Z}\Rightarrow\mathrm{x}^{\mathrm{4}} \in\mathbb{N} \\ $$$$\Rightarrow\mathrm{x}\in\mathbb{Z}\:\mathrm{or}\:\mathrm{x}=\pm^{\mathrm{4}} \sqrt{\mathrm{a}},\:\mathrm{a}\in\mathbb{N} \\ $$$$\lfloor\mathrm{5x}^{\mathrm{2}} \rfloor=\mathrm{n}\Rightarrow\mathrm{5x}^{\mathrm{2}} =\mathrm{n}+\theta,\:\mathrm{n}\in\mathbb{Z},\:\mathrm{0}\leqslant\theta<\mathrm{1} \\ $$$$\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{n}+\theta}{\mathrm{5}} \\ $$$$\mathrm{x}^{\mathrm{4}} =\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{2n}\theta+\theta^{\mathrm{2}} }{\mathrm{25}} \\ $$$$\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{2n}\theta+\theta^{\mathrm{2}} }{\mathrm{25}}−\mathrm{n}+\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{n}^{\mathrm{2}} +\left(\mathrm{2}\theta−\mathrm{25}\right)\mathrm{n}+\mathrm{100}+\theta^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{n}=\frac{\mathrm{25}−\mathrm{2}\theta\pm\sqrt{\mathrm{225}−\mathrm{100}\theta}}{\mathrm{2}}\in\mathbb{Z} \\ $$$$\mathrm{since}\:\mathrm{0}\leqslant\theta<\mathrm{1}\:\mathrm{so}: \\ $$$$\mathrm{I}\:\mathrm{case}: \\ $$$$\mathrm{15}\geqslant\sqrt{\mathrm{225}−\mathrm{100}\theta}>\mathrm{11} \\ $$$$\Rightarrow\mathrm{40}\geqslant\mathrm{40}−\mathrm{2}\theta\geqslant\mathrm{25}−\mathrm{2}\theta+\sqrt{\mathrm{225}−\mathrm{100}\theta}>\mathrm{36}−\mathrm{2}\theta>\mathrm{34} \\ $$$$\Rightarrow\mathrm{20}\geqslant\mathrm{n}>\mathrm{17}\therefore\mathrm{n}\in\left\{\mathrm{18},\mathrm{19},\mathrm{20}\right\} \\ $$$$\mathrm{II}\:\mathrm{case}: \\ $$$$\mathrm{8}<\mathrm{10}−\mathrm{2}\theta\leqslant\mathrm{25}−\mathrm{2}\theta−\sqrt{\mathrm{225}−\mathrm{100}\theta}<\mathrm{14}−\mathrm{2}\theta\leqslant\mathrm{14} \\ $$$$\mathrm{4}<\mathrm{n}<\mathrm{7}\Rightarrow\mathrm{n}\in\left\{\mathrm{5},\mathrm{6}\right\} \\ $$$$\Rightarrow\mathrm{n}=\mathrm{5} \\ $$$$\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{5}+\theta}{\mathrm{5}}=\mathrm{1}+\frac{\theta}{\mathrm{5}}\Rightarrow\mathrm{1}\leqslant\mathrm{x}^{\mathrm{2}} <\frac{\mathrm{6}}{\mathrm{5}}=\mathrm{1}.\mathrm{2} \\ $$$$\mathrm{x}=\pm\mathrm{1} \\ $$$$\Rightarrow\mathrm{n}=\mathrm{6}\left(\mathrm{no}\:\mathrm{sol}.\right) \\ $$$$\Rightarrow\mathrm{n}=\mathrm{18} \\ $$$$\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{18}+\theta}{\mathrm{5}}\Rightarrow\mathrm{3}.\mathrm{6}\leqslant\mathrm{x}^{\mathrm{2}} <\mathrm{3}.\mathrm{8}\Rightarrow\mathrm{x}\notin\mathbb{N} \\ $$$$\mathrm{x}^{\mathrm{2}} =\sqrt{\mathrm{a}},\:\mathrm{a}\in\mathbb{N}\Rightarrow\mathrm{3}.\mathrm{6}^{\mathrm{2}} \leqslant\mathrm{a}<\mathrm{3}.\mathrm{8}^{\mathrm{2}} \Rightarrow\mathrm{a}\in\left\{\mathrm{13},\mathrm{14}\right\} \\ $$$$\Rightarrow\mathrm{x}=\pm^{\mathrm{4}} \sqrt{\mathrm{14}} \\ $$$$\Rightarrow\mathrm{n}=\mathrm{19} \\ $$$$\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{19}+\theta}{\mathrm{5}}\Rightarrow\mathrm{3}.\mathrm{8}\leqslant\mathrm{x}^{\mathrm{2}} <\mathrm{4}\Rightarrow\mathrm{x}\notin\mathbb{N} \\ $$$$\mathrm{x}^{\mathrm{2}} =\sqrt{\mathrm{a}}\:\Rightarrow\mathrm{3}.\mathrm{8}^{\mathrm{2}} \leqslant\mathrm{a}<\mathrm{16}\Rightarrow\mathrm{a}=\mathrm{15} \\ $$$$\Rightarrow\mathrm{x}=\pm^{\mathrm{4}} \sqrt{\mathrm{15}} \\ $$$$\mathrm{n}=\mathrm{20} \\ $$$$\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{20}+\theta}{\mathrm{5}}\Rightarrow\mathrm{4}\leqslant\mathrm{x}^{\mathrm{2}} <\mathrm{5}\Rightarrow\mathrm{x}=\pm\mathrm{2} \\ $$$$\mathrm{all}\:\mathrm{the}\:\mathrm{solutions}\:\mathrm{are}: \\ $$$$\mathrm{x}=\left\{\pm\mathrm{1},\:\pm^{\mathrm{4}} \sqrt{\mathrm{14}},\:\pm^{\mathrm{4}} \sqrt{\mathrm{15}},\:\pm\mathrm{2}\right\} \\ $$

Commented by Dwaipayan Shikari last updated on 12/Oct/20

$${Thanking}\:{all}\:{of}\:{you} \\ $$

Answered by MJS_new last updated on 12/Oct/20

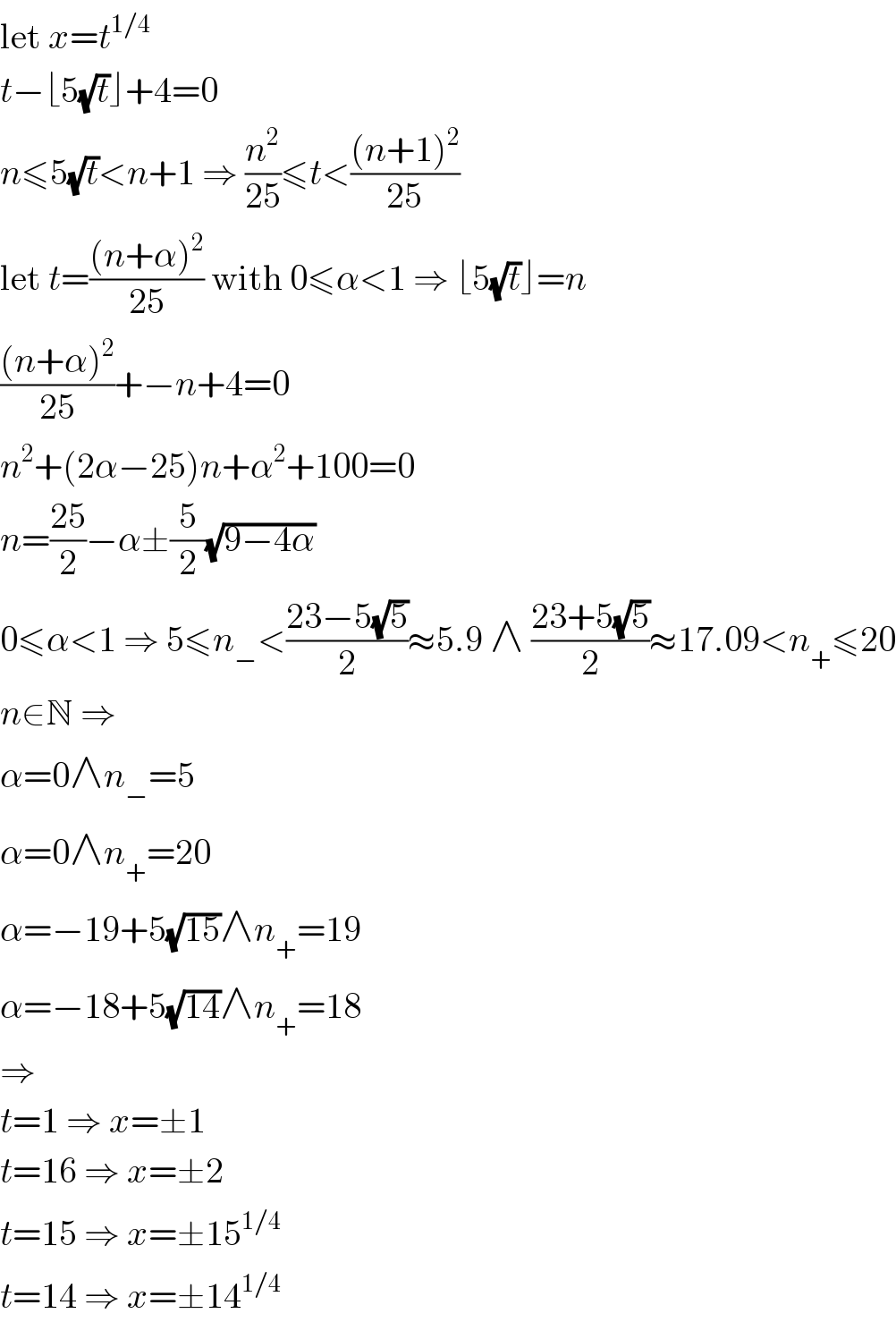
let x=t^(1/4) t−⌊5(√t)⌋+4=0 n≤5(√t)<n+1 ⇒ (n^2 /(25))≤t<(((n+1)^2 )/(25)) let t=(((n+α)^2 )/(25)) with 0≤α<1 ⇒ ⌊5(√t)⌋=n (((n+α)^2 )/(25))+−n+4=0 n^2 +(2α−25)n+α^2 +100=0 n=((25)/2)−α±(5/2)(√(9−4α)) 0≤α<1 ⇒ 5≤n_− <((23−5(√5))/2)≈5.9 ∧ ((23+5(√5))/2)≈17.09<n_+ ≤20 n∈N ⇒ α=0∧n_− =5 α=0∧n_+ =20 α=−19+5(√(15))∧n_+ =19 α=−18+5(√(14))∧n_+ =18 ⇒ t=1 ⇒ x=±1 t=16 ⇒ x=±2 t=15 ⇒ x=±15^(1/4) t=14 ⇒ x=±14^(1/4)

$$\mathrm{let}\:{x}={t}^{\mathrm{1}/\mathrm{4}} \\ $$$${t}−\lfloor\mathrm{5}\sqrt{{t}}\rfloor+\mathrm{4}=\mathrm{0} \\ $$$${n}\leqslant\mathrm{5}\sqrt{{t}}<{n}+\mathrm{1}\:\Rightarrow\:\frac{{n}^{\mathrm{2}} }{\mathrm{25}}\leqslant{t}<\frac{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{25}} \\ $$$$\mathrm{let}\:{t}=\frac{\left({n}+\alpha\right)^{\mathrm{2}} }{\mathrm{25}}\:\mathrm{with}\:\mathrm{0}\leqslant\alpha<\mathrm{1}\:\Rightarrow\:\lfloor\mathrm{5}\sqrt{{t}}\rfloor={n} \\ $$$$\frac{\left({n}+\alpha\right)^{\mathrm{2}} }{\mathrm{25}}+−{n}+\mathrm{4}=\mathrm{0} \\ $$$${n}^{\mathrm{2}} +\left(\mathrm{2}\alpha−\mathrm{25}\right){n}+\alpha^{\mathrm{2}} +\mathrm{100}=\mathrm{0} \\ $$$${n}=\frac{\mathrm{25}}{\mathrm{2}}−\alpha\pm\frac{\mathrm{5}}{\mathrm{2}}\sqrt{\mathrm{9}−\mathrm{4}\alpha} \\ $$$$\mathrm{0}\leqslant\alpha<\mathrm{1}\:\Rightarrow\:\mathrm{5}\leqslant{n}_{−} <\frac{\mathrm{23}−\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{2}}\approx\mathrm{5}.\mathrm{9}\:\wedge\:\frac{\mathrm{23}+\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{2}}\approx\mathrm{17}.\mathrm{09}<{n}_{+} \leqslant\mathrm{20} \\ $$$${n}\in\mathbb{N}\:\Rightarrow \\ $$$$\alpha=\mathrm{0}\wedge{n}_{−} =\mathrm{5} \\ $$$$\alpha=\mathrm{0}\wedge{n}_{+} =\mathrm{20} \\ $$$$\alpha=−\mathrm{19}+\mathrm{5}\sqrt{\mathrm{15}}\wedge{n}_{+} =\mathrm{19} \\ $$$$\alpha=−\mathrm{18}+\mathrm{5}\sqrt{\mathrm{14}}\wedge{n}_{+} =\mathrm{18} \\ $$$$\Rightarrow \\ $$$${t}=\mathrm{1}\:\Rightarrow\:{x}=\pm\mathrm{1} \\ $$$${t}=\mathrm{16}\:\Rightarrow\:{x}=\pm\mathrm{2} \\ $$$${t}=\mathrm{15}\:\Rightarrow\:{x}=\pm\mathrm{15}^{\mathrm{1}/\mathrm{4}} \\ $$$${t}=\mathrm{14}\:\Rightarrow\:{x}=\pm\mathrm{14}^{\mathrm{1}/\mathrm{4}} \\ $$

Commented by MJS_new last updated on 12/Oct/20

$$\mathrm{tried}\:\mathrm{to}\:\mathrm{find}\:\mathrm{a}\:\mathrm{shorter}\:\mathrm{path}… \\ $$

Answered by 1549442205PVT last updated on 13/Oct/20

x^4 −⌊5x^2 ⌋+4=0(1).Put x^4 +4=t(t≥4) ⇒x^2 =(√(t−4)).Then(1)⇔[5(√(t−4))]=t(∗) By the definition of function [x]we have 0≤5(√(t−4))−t<1 ⇔ { ((5(√(t−4))≥t(1))),((5(√(t−4))<t+1(2))) :}(∗∗) (1)⇔25(t−4)≥t^2 ⇔t^2 −25t+100≤0 ⇔(t−5)(t−20)≤0⇔5≤t≤20.Since t≥4,so by(∗)⇒t∈N⇒t∈{5,6,...,20}(3) (2)⇔25(t−4)<t^2 +2t+1 ⇔t^2 −23t+101>0⇔ t∈(−∞,((23−5(√5))/2))∪(((23+5(√5))/2),+∞) 5.9≈((23−5(√5))/2) and ((23+5(√5))/2)≈17.09 ⇒t∈{4,5}∪{18,19,20,21,...}(4) Combining (3)(4)we get t∈{5,18,19,20}are roots of the system of the inequalities (∗∗) i)t=5⇔x^4 +4=5⇔x^4 =1⇔x=±1 ii)t=18⇒x^4 +4=18⇔x=±^4 (√(14)) iii)t=19⇒x^4 +4=19⇔x=±^4 (√(15)) iv)t=20⇒x^4 +4=20⇔x=±2 Thus,roots of the system (∗∗) are x∈{±1;±2,±^4 (√(14)), ±^4 (√(15))}that is answer of our problem.

$${x}^{\mathrm{4}} −\lfloor\mathrm{5}{x}^{\mathrm{2}} \rfloor+\mathrm{4}=\mathrm{0}\left(\mathrm{1}\right).\mathrm{Put}\:\mathrm{x}^{\mathrm{4}} +\mathrm{4}=\mathrm{t}\left(\mathrm{t}\geqslant\mathrm{4}\right) \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} =\sqrt{\mathrm{t}−\mathrm{4}}.\mathrm{Then}\left(\mathrm{1}\right)\Leftrightarrow\left[\mathrm{5}\sqrt{\mathrm{t}−\mathrm{4}}\right]=\mathrm{t}\left(\ast\right) \\ $$$$\mathrm{By}\:\mathrm{the}\:\mathrm{definition}\:\mathrm{of}\:\mathrm{function}\:\left[\mathrm{x}\right]\mathrm{we} \\ $$$$\mathrm{have}\:\mathrm{0}\leqslant\mathrm{5}\sqrt{\mathrm{t}−\mathrm{4}}−\mathrm{t}<\mathrm{1} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{5}\sqrt{\mathrm{t}−\mathrm{4}}\geqslant\mathrm{t}\left(\mathrm{1}\right)}\\{\mathrm{5}\sqrt{\mathrm{t}−\mathrm{4}}<\mathrm{t}+\mathrm{1}\left(\mathrm{2}\right)}\end{cases}\left(\ast\ast\right) \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\mathrm{25}\left(\mathrm{t}−\mathrm{4}\right)\geqslant\mathrm{t}^{\mathrm{2}} \Leftrightarrow\mathrm{t}^{\mathrm{2}} −\mathrm{25t}+\mathrm{100}\leqslant\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{t}−\mathrm{5}\right)\left(\mathrm{t}−\mathrm{20}\right)\leqslant\mathrm{0}\Leftrightarrow\mathrm{5}\leqslant\mathrm{t}\leqslant\mathrm{20}.\mathrm{Since} \\ $$$$\mathrm{t}\geqslant\mathrm{4},\mathrm{so}\:\mathrm{by}\left(\ast\right)\Rightarrow\mathrm{t}\in\mathrm{N}\Rightarrow\mathrm{t}\in\left\{\mathrm{5},\mathrm{6},…,\mathrm{20}\right\}\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{2}\right)\Leftrightarrow\mathrm{25}\left(\mathrm{t}−\mathrm{4}\right)<\mathrm{t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{1} \\ $$$$\Leftrightarrow\mathrm{t}^{\mathrm{2}} −\mathrm{23t}+\mathrm{101}>\mathrm{0}\Leftrightarrow \\ $$$$\mathrm{t}\in\left(−\infty,\frac{\mathrm{23}−\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\cup\left(\frac{\mathrm{23}+\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{2}},+\infty\right) \\ $$$$\mathrm{5}.\mathrm{9}\approx\frac{\mathrm{23}−\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{2}}\:\mathrm{and}\:\frac{\mathrm{23}+\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{2}}\approx\mathrm{17}.\mathrm{09} \\ $$$$\Rightarrow\mathrm{t}\in\left\{\mathrm{4},\mathrm{5}\right\}\cup\left\{\mathrm{18},\mathrm{19},\mathrm{20},\mathrm{21},…\right\}\left(\mathrm{4}\right) \\ $$$$\mathrm{Combining}\:\left(\mathrm{3}\right)\left(\mathrm{4}\right)\mathrm{we}\:\mathrm{get}\: \\ $$$$\mathrm{t}\in\left\{\mathrm{5},\mathrm{18},\mathrm{19},\mathrm{20}\right\}\mathrm{are}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\: \\ $$$$\mathrm{system}\:\mathrm{of}\:\mathrm{the}\:\mathrm{inequalities}\:\left(\ast\ast\right) \\ $$$$\left.\mathrm{i}\right)\mathrm{t}=\mathrm{5}\Leftrightarrow\mathrm{x}^{\mathrm{4}} +\mathrm{4}=\mathrm{5}\Leftrightarrow\mathrm{x}^{\mathrm{4}} =\mathrm{1}\Leftrightarrow\mathrm{x}=\pm\mathrm{1} \\ $$$$\left.\mathrm{ii}\right)\mathrm{t}=\mathrm{18}\Rightarrow\mathrm{x}^{\mathrm{4}} +\mathrm{4}=\mathrm{18}\Leftrightarrow\mathrm{x}=\pm\:^{\mathrm{4}} \sqrt{\mathrm{14}} \\ $$$$\left.\mathrm{iii}\right)\mathrm{t}=\mathrm{19}\Rightarrow\mathrm{x}^{\mathrm{4}} +\mathrm{4}=\mathrm{19}\Leftrightarrow\mathrm{x}=\pm^{\mathrm{4}} \sqrt{\mathrm{15}} \\ $$$$\left.\mathrm{iv}\right)\mathrm{t}=\mathrm{20}\Rightarrow\mathrm{x}^{\mathrm{4}} +\mathrm{4}=\mathrm{20}\Leftrightarrow\mathrm{x}=\pm\mathrm{2} \\ $$$$\mathrm{Thus},\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{system}\:\left(\ast\ast\right)\:\mathrm{are} \\ $$$$\mathrm{x}\in\left\{\pm\mathrm{1};\pm\mathrm{2},\pm\:^{\mathrm{4}} \sqrt{\mathrm{14}},\:\pm\:^{\mathrm{4}} \sqrt{\mathrm{15}}\right\}\mathrm{that}\:\mathrm{is} \\ $$$$\mathrm{answer}\:\mathrm{of}\:\mathrm{our}\:\mathrm{problem}. \\ $$

Commented by floor(10²Eta[1]) last updated on 13/Oct/20

±^4 (√(14)) and ±^4 (√(15)) are solutions too

$$\pm^{\mathrm{4}} \sqrt{\mathrm{14}}\:\mathrm{and}\:\pm^{\mathrm{4}} \sqrt{\mathrm{15}}\:\mathrm{are}\:\mathrm{solutions}\:\mathrm{too} \\ $$

Commented by 1549442205PVT last updated on 13/Oct/20

$$\mathrm{I}\:\mathrm{mistaked}\:\mathrm{and}\:\mathrm{corrected}.\mathrm{Thank}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply