Menu Close

x-4-5x-3-6x-2-18-x-3-3x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 121696 by bemath last updated on 11/Nov/20
∫ ((x^4 −5x^3 +6x^2 −18)/(x^3 −3x^2 )) dx ?
$$\:\:\int\:\frac{{x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} −\mathrm{18}}{{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} }\:{dx}\:? \\ $$
Answered by liberty last updated on 11/Nov/20
J=∫ [(x−2)−((18)/(x^2 (x−3))) ]dx = J=(1/2)(x−2)^2 −18∫ (1/(x^2 (x−3))) dx Partial fraction (1/(x^2 (x−3))) = (A/x) + (B/x^2 ) + (C/(x−3)) C = [ (1/x^2 ) ]_(x=3) = (1/9) B = [ (1/(x−3)) ]_(x=0) = −(1/3) ⇔1 = Ax(x−3) −(1/3)(x−3)+(1/9)x^2 x=1⇒1 = −2A +(2/3)+(1/9) ⇒A=−(1/9) J = (((x−2)^2 )/2)−18∫ (−(1/(9x))+(1/(9(x−3)))−(1/(3x^2 ))) dx J = (((x−2)^2 )/2)+2ln ∣x∣ −2ln ∣x−3∣ −(6/x) + c . ▲
$$\mathrm{J}=\int\:\left[\left(\mathrm{x}−\mathrm{2}\right)−\frac{\mathrm{18}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}−\mathrm{3}\right)}\:\right]\mathrm{dx}\:= \\ $$$$\:\mathrm{J}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{18}\int\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}−\mathrm{3}\right)}\:\mathrm{dx}\: \\ $$$$\:\mathrm{Partial}\:\mathrm{fraction}\: \\ $$$$\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}−\mathrm{3}\right)}\:=\:\frac{\mathrm{A}}{\mathrm{x}}\:+\:\frac{\mathrm{B}}{\mathrm{x}^{\mathrm{2}} }\:+\:\frac{\mathrm{C}}{\mathrm{x}−\mathrm{3}} \\ $$$$\mathrm{C}\:=\:\left[\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:\right]_{\mathrm{x}=\mathrm{3}} =\:\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$\mathrm{B}\:=\:\left[\:\frac{\mathrm{1}}{\mathrm{x}−\mathrm{3}}\:\right]_{\mathrm{x}=\mathrm{0}} =\:−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Leftrightarrow\mathrm{1}\:=\:\mathrm{Ax}\left(\mathrm{x}−\mathrm{3}\right)\:−\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{x}−\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{9}}\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{x}=\mathrm{1}\Rightarrow\mathrm{1}\:=\:−\mathrm{2A}\:+\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{9}}\:\Rightarrow\mathrm{A}=−\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$\mathrm{J}\:=\:\frac{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{2}}−\mathrm{18}\int\:\left(−\frac{\mathrm{1}}{\mathrm{9x}}+\frac{\mathrm{1}}{\mathrm{9}\left(\mathrm{x}−\mathrm{3}\right)}−\frac{\mathrm{1}}{\mathrm{3x}^{\mathrm{2}} }\right)\:\mathrm{dx} \\ $$$$\mathrm{J}\:=\:\frac{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2ln}\:\mid\mathrm{x}\mid\:−\mathrm{2ln}\:\mid\mathrm{x}−\mathrm{3}\mid\:−\frac{\mathrm{6}}{\mathrm{x}}\:+\:\mathrm{c}\:.\:\blacktriangle\: \\ $$
Commented by bemath last updated on 11/Nov/20
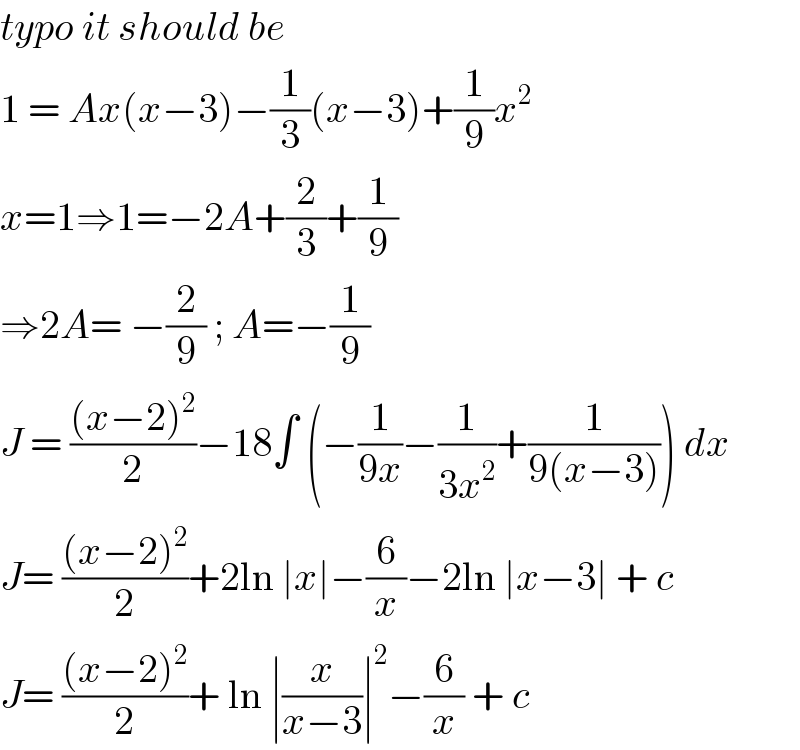
typo it should be 1 = Ax(x−3)−(1/3)(x−3)+(1/9)x^2 x=1⇒1=−2A+(2/3)+(1/9) ⇒2A= −(2/9) ; A=−(1/9) J = (((x−2)^2 )/2)−18∫ (−(1/(9x))−(1/(3x^2 ))+(1/(9(x−3)))) dx J= (((x−2)^2 )/2)+2ln ∣x∣−(6/x)−2ln ∣x−3∣ + c J= (((x−2)^2 )/2)+ ln ∣(x/(x−3))∣^2 −(6/x) + c
$${typo}\:{it}\:{should}\:{be}\: \\ $$$$\mathrm{1}\:=\:{Ax}\left({x}−\mathrm{3}\right)−\frac{\mathrm{1}}{\mathrm{3}}\left({x}−\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{9}}{x}^{\mathrm{2}} \\ $$$${x}=\mathrm{1}\Rightarrow\mathrm{1}=−\mathrm{2}{A}+\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$\Rightarrow\mathrm{2}{A}=\:−\frac{\mathrm{2}}{\mathrm{9}}\:;\:{A}=−\frac{\mathrm{1}}{\mathrm{9}} \\ $$$${J}\:=\:\frac{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{2}}−\mathrm{18}\int\:\left(−\frac{\mathrm{1}}{\mathrm{9}{x}}−\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{9}\left({x}−\mathrm{3}\right)}\right)\:{dx} \\ $$$${J}=\:\frac{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2ln}\:\mid{x}\mid−\frac{\mathrm{6}}{{x}}−\mathrm{2ln}\:\mid{x}−\mathrm{3}\mid\:+\:{c} \\ $$$${J}=\:\frac{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{2}}+\:\mathrm{ln}\:\mid\frac{{x}}{{x}−\mathrm{3}}\mid^{\mathrm{2}} −\frac{\mathrm{6}}{{x}}\:+\:{c}\: \\ $$
Answered by MJS_new last updated on 11/Nov/20
∫((x^4 −5x^3 +6x^2 −18)/(x^3 −3x^2 ))dx= =∫x−2+(2/x)−(2/(x−3))+(6/x^2 )dx= =(x^2 /2)−2x+2ln ∣x∣ −2ln ∣x−3∣ −(6/x)= =((x^3 −4x^2 −12)/(2x))+2ln ∣(x/(x−3))∣ +C
$$\int\frac{{x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} −\mathrm{18}}{{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} }{dx}= \\ $$$$=\int{x}−\mathrm{2}+\frac{\mathrm{2}}{{x}}−\frac{\mathrm{2}}{{x}−\mathrm{3}}+\frac{\mathrm{6}}{{x}^{\mathrm{2}} }{dx}= \\ $$$$=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}{x}+\mathrm{2ln}\:\mid{x}\mid\:−\mathrm{2ln}\:\mid{x}−\mathrm{3}\mid\:−\frac{\mathrm{6}}{{x}}= \\ $$$$=\frac{{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} −\mathrm{12}}{\mathrm{2}{x}}+\mathrm{2ln}\:\mid\frac{{x}}{{x}−\mathrm{3}}\mid\:+{C} \\ $$
Commented by liberty last updated on 11/Nov/20
Ostrogradski
$$\mathrm{Ostrogradski}\: \\ $$
Commented by MJS_new last updated on 11/Nov/20
no. just decomposition.
$$\mathrm{no}.\:\mathrm{just}\:\mathrm{decomposition}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *