Menu Close

x-4-ax-2-bx-c-0-solve-for-x-

Tinku Tara 0 Comments
Pin




Question Number 65271 by ajfour last updated on 27/Jul/19
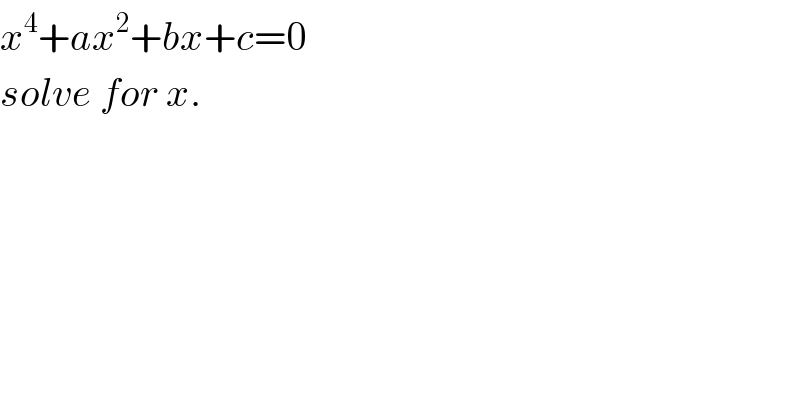
x^4 +ax^2 +bx+c=0 solve for x.
$${x}^{\mathrm{4}} +{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$${solve}\:{for}\:{x}. \\ $$
Answered by ajfour last updated on 29/Jul/19
let x^2 =px+t (px+t)^2 +a(px+t)+bx+c=0 p^2 (px+t)+t^2 +2ptx+a(px+t)+bx+c=0 ⇒ x(p^3 +2pt+ap+b) +t^2 +(p^2 +a)t+c=0 let coeff. of x be zero ⇒ t=−(((p^3 +ap+b))/(2p)) also then t^2 +(p^2 +a)t+c=0 ⇒ (p^3 +ap+b)^2 −2p(p^2 +a)(p^3 +ap+b)+4cp^2 =0 ⇒ p^6 +2ap^4 _(−) +2bp^3 _(−) +a^2 p^2 _(−) +2abp_(−) +b^2 −2p^6 −2ap^4 _(−) −2bp^3 _(−) −2ap^4 −2_− a^2 p^2 −2abp_(−) +4cp^2 =0 __________________________ p^6 +2ap^4 +(a^2 −4c)p^2 −b^2 =0 (its a cubic in p^2 ) Now t=−(((p^3 +ap+b))/(2p)) x^2 −px−t=0 _________________________■
$${let}\:{x}^{\mathrm{2}} ={px}+{t} \\ $$$$\left({px}+{t}\right)^{\mathrm{2}} +{a}\left({px}+{t}\right)+{bx}+{c}=\mathrm{0} \\ $$$${p}^{\mathrm{2}} \left({px}+{t}\right)+{t}^{\mathrm{2}} +\mathrm{2}{ptx}+{a}\left({px}+{t}\right)+{bx}+{c}=\mathrm{0} \\ $$$$\Rightarrow\:{x}\left({p}^{\mathrm{3}} +\mathrm{2}{pt}+{ap}+{b}\right) \\ $$$$\:\:\:\:\:\:+{t}^{\mathrm{2}} +\left({p}^{\mathrm{2}} +{a}\right){t}+{c}=\mathrm{0}\:\:\: \\ $$$${let}\:{coeff}.\:{of}\:{x}\:{be}\:{zero} \\ $$$$\Rightarrow\:\:\:{t}=−\frac{\left({p}^{\mathrm{3}} +{ap}+{b}\right)}{\mathrm{2}{p}} \\ $$$${also}\:\:{then} \\ $$$$\:\:\:\:\:\:\:\:{t}^{\mathrm{2}} +\left({p}^{\mathrm{2}} +{a}\right){t}+{c}=\mathrm{0} \\ $$$$\:\Rightarrow\:\:\left({p}^{\mathrm{3}} +{ap}+{b}\right)^{\mathrm{2}} \\ $$$$\:−\mathrm{2}{p}\left({p}^{\mathrm{2}} +{a}\right)\left({p}^{\mathrm{3}} +{ap}+{b}\right)+\mathrm{4}{cp}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow \\ $$$${p}^{\mathrm{6}} +\underset{−} {\mathrm{2}{ap}^{\mathrm{4}} }+\underset{−} {\mathrm{2}{bp}^{\mathrm{3}} }+\underset{−} {{a}^{\mathrm{2}} {p}^{\mathrm{2}} }+\underset{−} {\mathrm{2}{abp}}+{b}^{\mathrm{2}} \\ $$$$−\mathrm{2}{p}^{\mathrm{6}} −\underset{−} {\mathrm{2}{ap}^{\mathrm{4}} }−\underset{−} {\mathrm{2}{bp}^{\mathrm{3}} }−\mathrm{2}{ap}^{\mathrm{4}} −\underset{−} {\mathrm{2}}{a}^{\mathrm{2}} {p}^{\mathrm{2}} \\ $$$$−\underset{−} {\mathrm{2}{abp}}+\mathrm{4}{cp}^{\mathrm{2}} =\mathrm{0} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${p}^{\mathrm{6}} +\mathrm{2}{ap}^{\mathrm{4}} +\left({a}^{\mathrm{2}} −\mathrm{4}{c}\right){p}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({its}\:{a}\:{cubic}\:{in}\:{p}^{\mathrm{2}} \right) \\ $$$${Now}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{t}=−\frac{\left({p}^{\mathrm{3}} +{ap}+{b}\right)}{\mathrm{2}{p}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} −{px}−{t}=\mathrm{0} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\blacksquare \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *