x-4-c-3-x-3-c-2-x-2-c-1-x-c-0-0-for-c-n-R-this-can-have-4-unique-zeros-R-2-unique-zeros-1-double-zero-R-2-double-zeros-R-1-triple-1-unique-zeros-R-1-fourfold-zero-R-2-unique-zeros-R-1

FacebookTweetPin

Question Number 152625 by Dandelion last updated on 30/Aug/21

$$x^4+c_3{x}^3+c_2{x}^2+c_{1}x+c_0=0$$$$\mathrm{for}{c}_n\in \mathbb{R}\mathrm{this}\mathrm{can}\mathrm{have}$$$$4\mathrm{unique}\mathrm{zeros}\in \mathbb{R}$$$$2\mathrm{unique}\mathrm{zeros}+1\mathrm{double}\mathrm{zero}\in \mathbb{R}$$$$2\mathrm{double}\mathrm{zeros}\in \mathbb{R}$$$$1\mathrm{triple}+1\mathrm{unique}\mathrm{zeros}\in \mathbb{R}$$$$1\mathrm{fourfold}\mathrm{zero}\in \mathbb{R}$$$$2\mathrm{unique}\mathrm{zeros}\in \mathbb{R}+1\mathrm{pair}\mathrm{of}\mathrm{complex}\mathrm{zeros}$$$$1\mathrm{double}\mathrm{zero}\in \mathbb{R}+1\mathrm{pair}\mathrm{of}\mathrm{complex}\mathrm{zeros}$$$$2\mathrm{pairs}\mathrm{of}\mathrm{complex}\mathrm{zeros}$$$$2\mathrm{double}\mathrm{imaginary}\mathrm{zeros}$$$$$$$$\mathrm{for}\mathrm{given}{c}_n;\mathrm{can}\mathrm{we}\mathrm{decide}\mathrm{which}\mathrm{case}\mathrm{we}$$$$\mathrm{have}\mathrm{without}\mathrm{solving}?$$

Commented by Dandelion last updated on 30/Aug/21

$$\dots \mathrm{is}\mathrm{there}\mathrm{a}D\left(\mathrm{or}\mathrm{\Delta }\right)\mathrm{similar}\mathrm{to}\mathrm{polynomes}$$$$\mathrm{of}2\mathrm{nd}\mathrm{and}3\mathrm{rd}\mathrm{degree}?$$

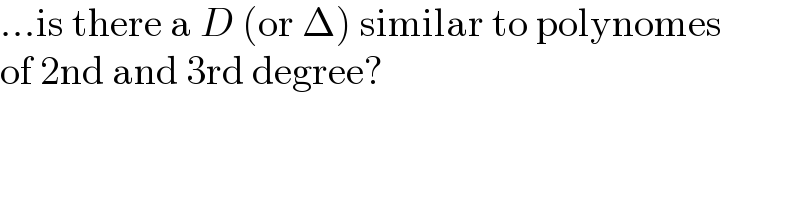
Commented by MJS_new last updated on 31/Aug/21

$${\mathrm{it}}^{\prime }\mathrm{s}\mathrm{a}\mathrm{bit}\mathrm{complicated}.{\mathrm{I}}^{\prime }\mathrm{ll}\mathrm{post}\mathrm{the}\mathrm{answer}$$$$\mathrm{later}\dots$$

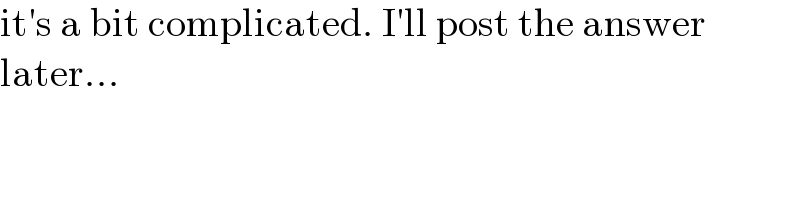
Answered by MJS_new last updated on 02/Sep/21

$$x^4+c_3{x}^3+c_2{x}^2+c_{1}x+c_0=0$$$$1.\mathrm{let}x=t-\frac{c_3}{4}\mathrm{and}\mathrm{rename}\mathrm{the}\mathrm{new}\mathrm{constants}$$$$\Rightarrow$$$$t^4+{pt}^2+qt+r=0$$$$$$$$D_1=16p^{4}r-4p^3{q}^2-128p^2{r}^2+144{pq}^{2}r-27q^4+256r^3$$$$D_2=p^2+12r$$$$D_3=-p^2+4r$$$$$$$$\left(1\right)D_1<0$$$$\Rightarrow 2\mathrm{unique}\mathrm{real}+1\mathrm{pair}\mathrm{of}\mathrm{conjugated}\mathrm{complex}\mathrm{solutions}$$$$$$$$\left(2\right)D_1>0\wedge p<0\wedge D_3<0$$$$\Rightarrow 4\mathrm{unique}\mathrm{real}\mathrm{solutions}$$$$$$$$\left(3\right)D_1>0\wedge (p>0\vee D_3>0)$$$$\Rightarrow 2\mathrm{pairs}\mathrm{of}\mathrm{conjugated}\mathrm{complex}\mathrm{solutions}$$$$$$$$\left(4\right)D_1=0\wedge p<0\wedge D_3<0\wedge D_2\ne 0$$$$\Rightarrow 1\mathrm{real}\mathrm{double}+2\mathrm{unique}\mathrm{real}\mathrm{solutions}$$$$$$$$\left(5\right)D_1=0\wedge (D_3>0\vee p>0\wedge (D_3\ne 0\vee q\ne 0))$$$$\Rightarrow 1\mathrm{real}\mathrm{double}+1\mathrm{pair}\mathrm{of}\mathrm{conjugated}\mathrm{complex}\mathrm{solutions}$$$$$$$$\left(6\right)D_1=0\wedge D_2=0\wedge D_3\ne 0$$$$\Rightarrow 1\mathrm{real}\mathrm{triple}+1\mathrm{unique}\mathrm{real}\mathrm{solutions}$$$$$$$$\left(7\right)D_1=0\wedge D_3=0\wedge p<0$$$$\Rightarrow 2\mathrm{real}\mathrm{double}\mathrm{solutions}$$$$$$$$\left(8\right)D_1=0\wedge D_3=0\wedge p>0\wedge q=0$$$$\Rightarrow 2\mathrm{imaginary}\mathrm{double}\mathrm{solutions}$$$$$$$$\left(9\right)D_1=0\wedge D_2=0$$$$\Rightarrow 1\mathrm{real}\mathrm{fourfold}\mathrm{solution}$$

Commented by Tawa11 last updated on 02/Sep/21

$$\mathrm{Great}\mathrm{sir}$$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

FacebookTweetPin