Menu Close

x-4-dx-x-8-x-4-1-

Tinku Tara 0 Comments
Pin




Question Number 95436 by 675480065 last updated on 25/May/20
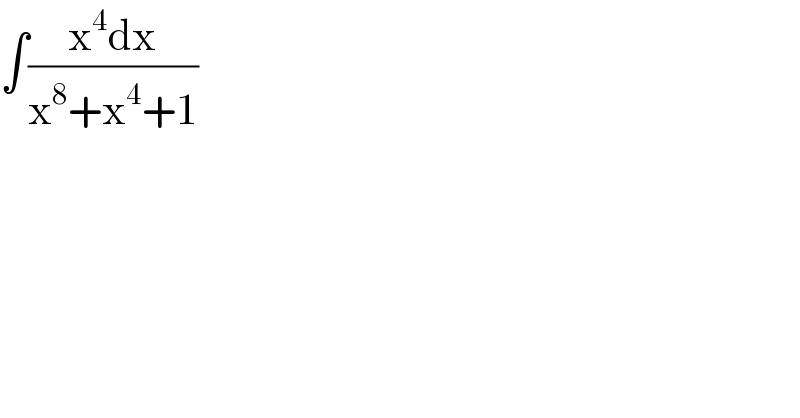
∫((x^4 dx)/(x^8 +x^4 +1))
$$\int\frac{\mathrm{x}^{\mathrm{4}} \mathrm{dx}}{\mathrm{x}^{\mathrm{8}} +\mathrm{x}^{\mathrm{4}} +\mathrm{1}} \\ $$
Answered by Mr.D.N. last updated on 25/May/20
I= ∫ ((x^4 dx)/(x^8 +x^4 +1)) =∫ ((x^4 dx)/(x^4 (x^4 +1+(1/x^4 )))) = ∫ (( 1)/(x^4 +(1/x^4 )+1))dx = ∫ (1/((x^2 +(1/x^2 ))^2 −2+1))dx=∫ (1/((x^2 +(1/x^2 ))^2 −(1)^2 ))dx =∫ (1/((x^2 +(1/x^2 )+1)(x^2 +(1/x^2 ) −1)))dx = (1/2)∫ (1/(x^2 +(1/x^2 ) −1))dx − (1/2)∫ (( 1)/(x^2 +(1/x^2 ) +1))dx = (1/2) ∫ (1/((x+(1/x))^2 −2−1))dx−(1/2)∫ (( 1)/((x−(1/x))^2 +2−1))dx = (1/2) ∫ (( 1)/((x+(1/x))^2 −3))dx − (1/2)∫ (( 1)/((x −(1/x))^2 +1))dx = (1/2)∫ (( 1)/((x+(1/x))^2 −((√3))^2 ))dx −(1/2)∫ (( 1)/((x−(1/x))^2 +(1)^2 ))dx = (1/2)[ (1/(2(√3))) log ((x+(1/x) −(√3))/(x+(1/x) +(√3)))] − (1/2)[ (1/( (√3))) tan^(−1) ((x−(1/x))/( (√3)))]+C = (1/(4(√3))) log ((x^2 −(√3) x +1)/(x^2 +(√3)x +1)) − (1/(2(√3))) tan^(−1) ((x^2 −1)/( (√3) x)) +C //.
$$\:\:\:\:\mathrm{I}=\:\int\:\frac{\mathrm{x}^{\mathrm{4}} \mathrm{dx}}{\mathrm{x}^{\mathrm{8}} +\mathrm{x}^{\mathrm{4}} +\mathrm{1}} \\ $$$$\:\:\:\:\:\:=\int\:\frac{\mathrm{x}^{\mathrm{4}} \mathrm{dx}}{\mathrm{x}^{\mathrm{4}} \left(\mathrm{x}^{\mathrm{4}} +\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} }\right)}\:\:=\:\int\:\frac{\:\mathrm{1}}{\mathrm{x}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} }+\mathrm{1}}\mathrm{dx} \\ $$$$\:\:\:\:\:\:=\:\int\:\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)^{\mathrm{2}} −\mathrm{2}+\mathrm{1}}\mathrm{dx}=\int\:\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)^{\mathrm{2}} −\left(\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\:\:\:\:\:\:=\int\:\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:−\mathrm{1}\right)}\mathrm{dx} \\ $$$$\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:−\mathrm{1}}\mathrm{dx}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\:\:\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:+\mathrm{1}}\mathrm{dx} \\ $$$$\:\:\:\:\:=\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\mathrm{1}}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{2}−\mathrm{1}}\mathrm{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\:\mathrm{1}}{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} +\mathrm{2}−\mathrm{1}}\mathrm{dx} \\ $$$$\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\:\:\mathrm{1}}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{3}}\mathrm{dx}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\:\mathrm{1}}{\left(\mathrm{x}\:−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$\:\:\:\:=\:\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\:\:\mathrm{1}}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\mathrm{dx}\:−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\:\mathrm{1}}{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} +\left(\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\:\:\:\:\:=\:\:\frac{\mathrm{1}}{\mathrm{2}}\left[\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\:\mathrm{log}\:\frac{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\:−\sqrt{\mathrm{3}}}{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\:+\sqrt{\mathrm{3}}}\right]\:−\:\frac{\mathrm{1}}{\mathrm{2}}\left[\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}}{\:\sqrt{\mathrm{3}}}\right]+\mathrm{C} \\ $$$$\:\:=\:\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}\:\mathrm{log}\:\frac{\mathrm{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}\:\mathrm{x}\:+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}\mathrm{x}\:+\mathrm{1}}\:−\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{\mathrm{3}}\:\mathrm{x}}\:+\mathrm{C}\:\://. \\ $$$$\:\: \\ $$
Commented by PRITHWISH SEN 2 last updated on 25/May/20
sir I think it is ∫(dx/((x+(1/x))^2 −((√3))^2 )) so d(x+(1/x))=1−(1/x^2 ) ∫(dx/(x^2 −a^2 )) cannot be applied here.
$$\mathrm{sir}\:\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{is} \\ $$$$\int\frac{\mathrm{dx}}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\:\:\mathrm{so}\:\:\:\mathrm{d}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }\:\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{applied}\:\mathrm{here}. \\ $$
Commented by mathmax by abdo last updated on 25/May/20
∫ (dx/((x+(1/x))^2 −3)) =∫ ((1−(1/(x^2 ))+(1/x^2 ))/((x+(1/x))^2 −3))dx =∫ ((1−(1/x^2 ))/((x+(1/x))^2 −3))dx(x+(1/x)=u) +∫ (dx/(x^2 ((x+(1/x))^2 −3))) ∫ (du/(u^2 −3)) (solvable) +∫ (dx/(x^2 (x^2 +2+(1/x^2 )−3))) =∫ ...dx +∫ (dx/(x^4 +2x^2 +1−3x^2 )) =∫...dx +∫ (dx/(x^4 −x^2 +1)) and ∫ (dx/(x^4 −x^2 +1)) =∫ (dx/((x^2 +1)^2 −3x^2 )) =∫ (dx/((x^2 −(√3)x +1)(x^2 +(√3)x +1))) this integral is solvable by decomposition...
$$\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{3}}\:=\int\:\:\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{3}}\mathrm{dx} \\ $$$$=\int\:\:\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{3}}\mathrm{dx}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{u}\right)\:+\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \left(\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{3}\right)} \\ $$$$\int\:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} −\mathrm{3}}\:\left(\mathrm{solvable}\right)\:+\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{3}\right)} \\ $$$$=\int\:\:…\mathrm{dx}\:\:+\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} \:+\mathrm{2x}^{\mathrm{2}} +\mathrm{1}−\mathrm{3x}^{\mathrm{2}} }\:=\int…\mathrm{dx}\:+\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:\mathrm{and} \\ $$$$\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{3x}^{\mathrm{2}} }\:=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}\mathrm{x}\:+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}\mathrm{x}\:+\mathrm{1}\right)} \\ $$$$\mathrm{this}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{solvable}\:\mathrm{by}\:\mathrm{decomposition}… \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 25/May/20
sir m^r dn you answer is not correct!
$$\mathrm{sir}\:\mathrm{m}^{\mathrm{r}} \mathrm{dn}\:\mathrm{you}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{not}\:\mathrm{correct}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *