Question Number 144359 by mathdanisur last updated on 24/Jun/21
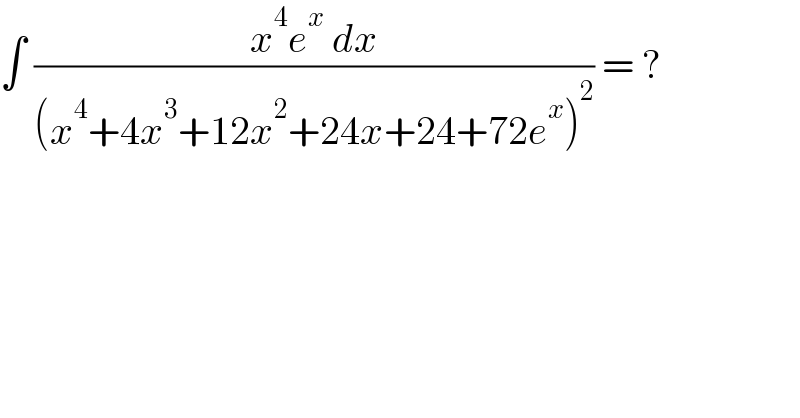
$$\int\:\frac{{x}^{\mathrm{4}} {e}^{{x}} \:{dx}}{\left({x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} +\mathrm{12}{x}^{\mathrm{2}} +\mathrm{24}{x}+\mathrm{24}+\mathrm{72}{e}^{{x}} \right)^{\mathrm{2}} }\:=\:? \\ $$
Answered by mitica last updated on 24/Jun/21
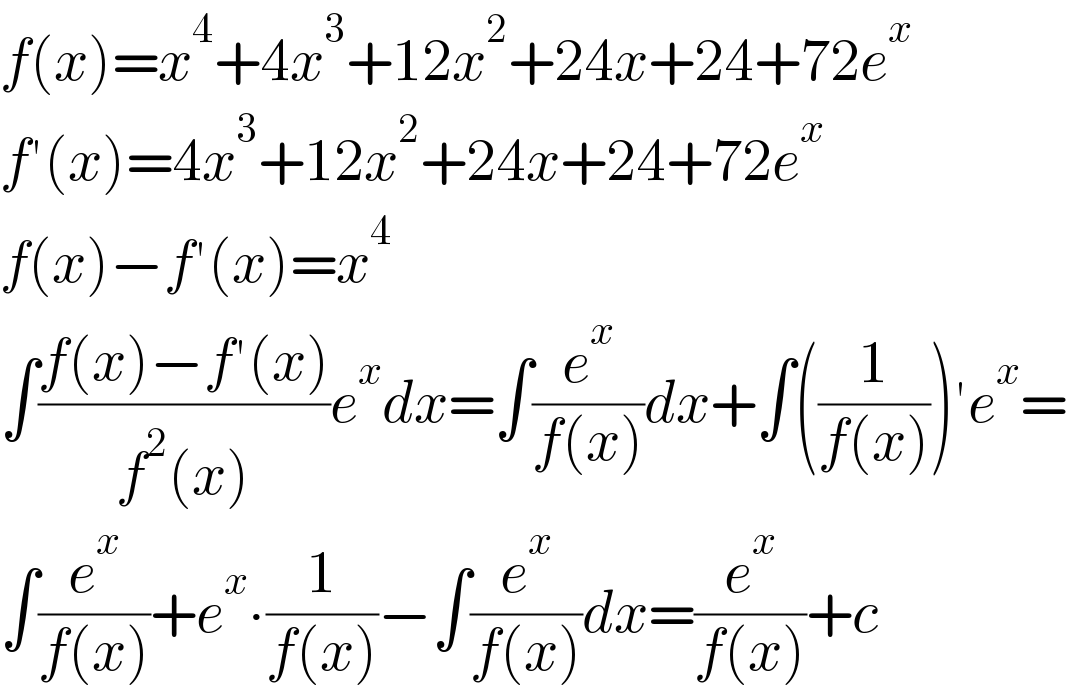
$${f}\left({x}\right)={x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} +\mathrm{12}{x}^{\mathrm{2}} +\mathrm{24}{x}+\mathrm{24}+\mathrm{72}{e}^{{x}} \\ $$$${f}'\left({x}\right)=\mathrm{4}{x}^{\mathrm{3}} +\mathrm{12}{x}^{\mathrm{2}} +\mathrm{24}{x}+\mathrm{24}+\mathrm{72}{e}^{{x}} \\ $$$${f}\left({x}\right)−{f}'\left({x}\right)={x}^{\mathrm{4}} \\ $$$$\int\frac{{f}\left({x}\right)−{f}'\left({x}\right)}{{f}^{\mathrm{2}} \left({x}\right)}{e}^{{x}} {dx}=\int\frac{{e}^{{x}} }{{f}\left({x}\right)}{dx}+\int\left(\frac{\mathrm{1}}{{f}\left({x}\right)}\right)'{e}^{{x}} = \\ $$$$\int\frac{{e}^{{x}} }{{f}\left({x}\right)}+{e}^{{x}} \centerdot\frac{\mathrm{1}}{{f}\left({x}\right)}−\int\frac{{e}^{{x}} }{{f}\left({x}\right)}{dx}=\frac{{e}^{{x}} }{{f}\left({x}\right)}+{c} \\ $$
Commented by mathdanisur last updated on 24/Jun/21
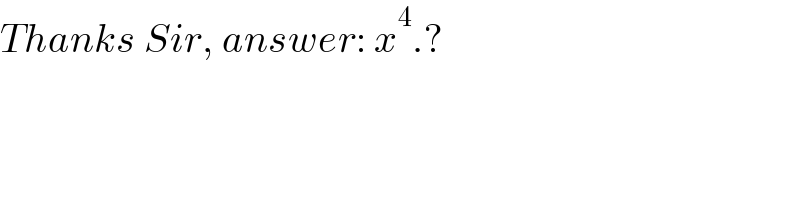
$${Thanks}\:{Sir},\:{answer}:\:{x}^{\mathrm{4}} .? \\ $$
Commented by mathdanisur last updated on 24/Jun/21
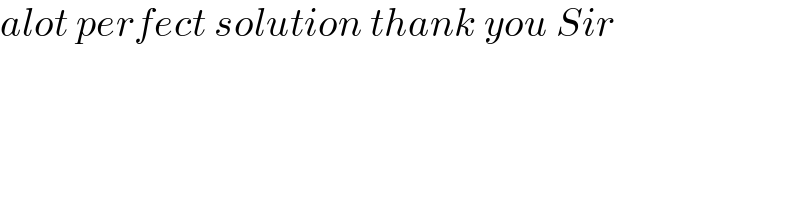
$${alot}\:{perfect}\:{solution}\:{thank}\:{you}\:{Sir} \\ $$
Commented by mitica last updated on 24/Jun/21

$$\frac{{e}^{{x}} }{{f}\left({x}\right)} \\ $$
