Question Number 128542 by bramlexs22 last updated on 08/Jan/21
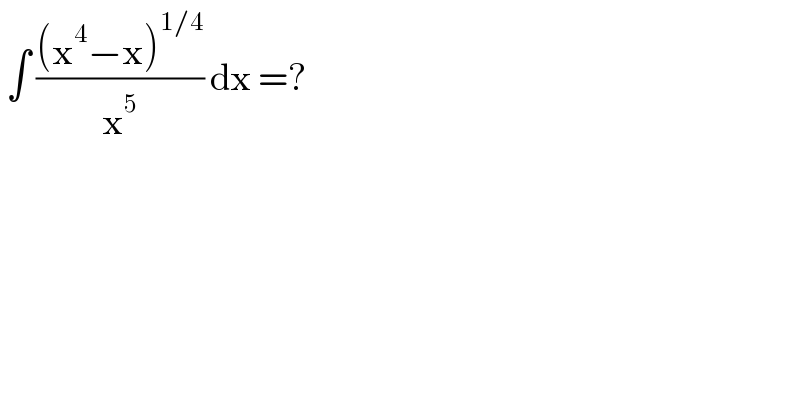
$$\:\int\:\frac{\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}\right)^{\mathrm{1}/\mathrm{4}} }{\mathrm{x}^{\mathrm{5}} }\:\mathrm{dx}\:=? \\ $$
Answered by liberty last updated on 08/Jan/21
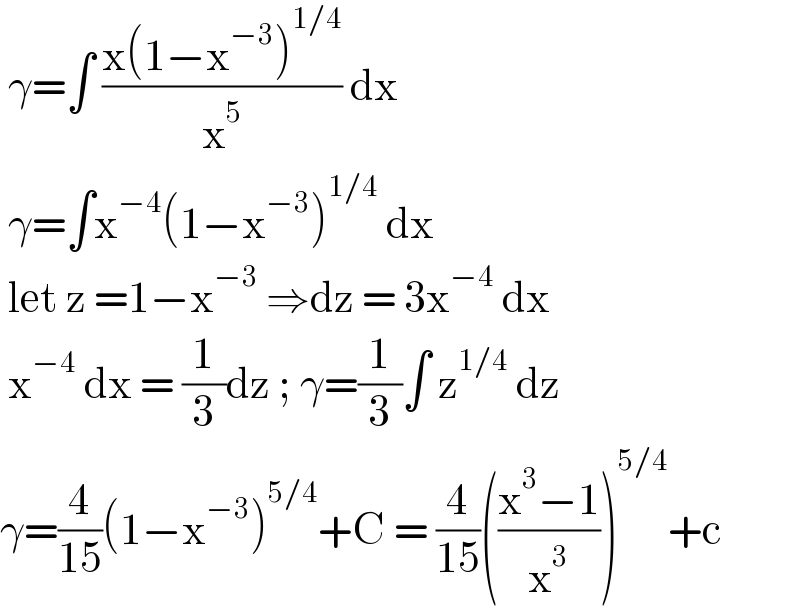
$$\:\gamma=\int\:\frac{\mathrm{x}\left(\mathrm{1}−\mathrm{x}^{−\mathrm{3}} \right)^{\mathrm{1}/\mathrm{4}} }{\mathrm{x}^{\mathrm{5}} }\:\mathrm{dx}\: \\ $$$$\:\gamma=\int\mathrm{x}^{−\mathrm{4}} \left(\mathrm{1}−\mathrm{x}^{−\mathrm{3}} \right)^{\mathrm{1}/\mathrm{4}} \:\mathrm{dx}\: \\ $$$$\:\mathrm{let}\:\mathrm{z}\:=\mathrm{1}−\mathrm{x}^{−\mathrm{3}} \:\Rightarrow\mathrm{dz}\:=\:\mathrm{3x}^{−\mathrm{4}} \:\mathrm{dx}\: \\ $$$$\:\mathrm{x}^{−\mathrm{4}} \:\mathrm{dx}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{dz}\:;\:\gamma=\frac{\mathrm{1}}{\mathrm{3}}\int\:\mathrm{z}^{\mathrm{1}/\mathrm{4}} \:\mathrm{dz}\: \\ $$$$\gamma=\frac{\mathrm{4}}{\mathrm{15}}\left(\mathrm{1}−\mathrm{x}^{−\mathrm{3}} \right)^{\mathrm{5}/\mathrm{4}} +\mathrm{C}\:=\:\frac{\mathrm{4}}{\mathrm{15}}\left(\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\right)^{\mathrm{5}/\mathrm{4}} +\mathrm{c} \\ $$
