Menu Close

x-4-x-2-1-x-2-4-2-x-2-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 118819 by bramlexs22 last updated on 20/Oct/20
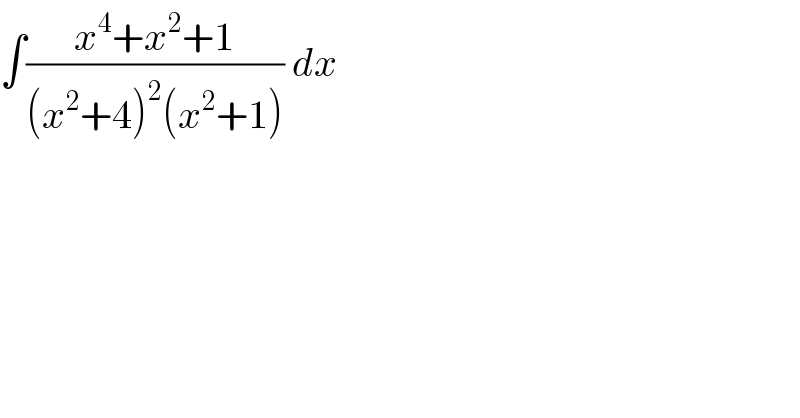
∫((x^4 +x^2 +1)/((x^2 +4)^2 (x^2 +1))) dx
$$\int\frac{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:{dx}\: \\ $$
Answered by MJS_new last updated on 20/Oct/20
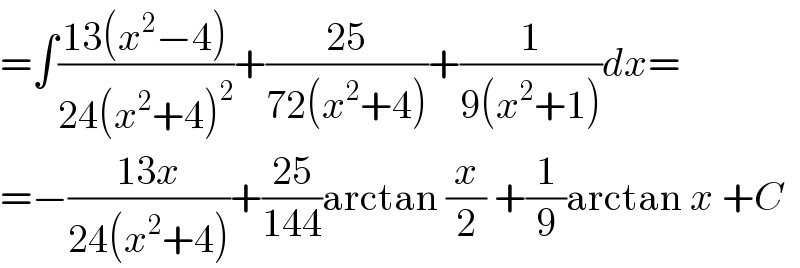
=∫((13(x^2 −4))/(24(x^2 +4)^2 ))+((25)/(72(x^2 +4)))+(1/(9(x^2 +1)))dx= =−((13x)/(24(x^2 +4)))+((25)/(144))arctan (x/2) +(1/9)arctan x +C
$$=\int\frac{\mathrm{13}\left({x}^{\mathrm{2}} −\mathrm{4}\right)}{\mathrm{24}\left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} }+\frac{\mathrm{25}}{\mathrm{72}\left({x}^{\mathrm{2}} +\mathrm{4}\right)}+\frac{\mathrm{1}}{\mathrm{9}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx}= \\ $$$$=−\frac{\mathrm{13}{x}}{\mathrm{24}\left({x}^{\mathrm{2}} +\mathrm{4}\right)}+\frac{\mathrm{25}}{\mathrm{144}}\mathrm{arctan}\:\frac{{x}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{9}}\mathrm{arctan}\:{x}\:+{C} \\ $$
Answered by bobhans last updated on 20/Oct/20
in other way by partial fraction ((x^4 +x^2 +1)/((x^2 +4)^2 (x^2 +1))) = ((ax+b)/(x^2 +1)) + ((cx+d)/(x^2 +4)) + ((ex+f)/((x^2 +4)^2 )) x^4 +x^2 +1 = (ax+b)(x^2 +4)^2 +(cx+d)(x^2 +1)(x^2 +4)+(ex+f)(x^2 +1) replacing x by −x yields x^4 +x^2 +1=(−ax+b)(x^2 +4)^2 +(−cx+d)(x^2 +1)(x^2 +4)+(−ex+f)(x^2 +1) from substracting these last two equation gives a=c=e=0 , d=(8/9), f=−((13)/3) therefore I=(1/9)∫(dx/(x^2 +1))+(4/9)∫((2 dx)/(x^2 +4))−((13)/3)∫ (dx/((x^2 +4)^2 )) I= (1/9) arc tan x +(4/9) arc tan ((x/2))−((13)/(48)) (arc tan ((x/2))+((2x)/(x^2 +4))) + C
$${in}\:{other}\:{way}\:{by}\:{partial}\:{fraction} \\ $$$$\:\frac{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:=\:\frac{{ax}+{b}}{{x}^{\mathrm{2}} +\mathrm{1}}\:+\:\frac{{cx}+{d}}{{x}^{\mathrm{2}} +\mathrm{4}}\:+\:\frac{{ex}+{f}}{\left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} } \\ $$$$\:{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}\:=\:\left({ax}+{b}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} +\left({cx}+{d}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)+\left({ex}+{f}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$${replacing}\:{x}\:{by}\:−{x}\:{yields} \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}=\left(−{ax}+{b}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} +\left(−{cx}+{d}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)+\left(−{ex}+{f}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$${from}\:{substracting}\:{these}\:{last}\:{two}\:{equation} \\ $$$${gives}\:{a}={c}={e}=\mathrm{0}\:,\:{d}=\frac{\mathrm{8}}{\mathrm{9}},\:{f}=−\frac{\mathrm{13}}{\mathrm{3}} \\ $$$${therefore}\:{I}=\frac{\mathrm{1}}{\mathrm{9}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{4}}{\mathrm{9}}\int\frac{\mathrm{2}\:{dx}}{{x}^{\mathrm{2}} +\mathrm{4}}−\frac{\mathrm{13}}{\mathrm{3}}\int\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} } \\ $$$${I}=\:\frac{\mathrm{1}}{\mathrm{9}}\:\mathrm{arc}\:\mathrm{tan}\:{x}\:+\frac{\mathrm{4}}{\mathrm{9}}\:\mathrm{arc}\:\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)−\frac{\mathrm{13}}{\mathrm{48}}\:\left(\mathrm{arc}\:\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)+\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{4}}\right)\:+\:{C} \\ $$
Answered by 1549442205PVT last updated on 21/Oct/20
((x^4 +x^2 +1)/((x^2 +4)^2 (x^2 +1))) =((ax^3 +bx^2 +cx+d)/(x^4 +8x^2 +16))+((ex+f)/(x^2 +1)) ⇔x^4 +x^2 +1=(a+e)x^5 +(b+f)x^4 +(a+c+8e)x^3 +(b+d+8f)x^2 +(c+16e)x+d+16f ⇔ { ((a+e=0)),((b+f=1)),((a+c+8e=0)),((b+d+8f=1)),((c+16e=0)),((d+16f=1)) :}⇔ { ((a=c=e=0)),((b=8/9)),((d=−7/9)),((f=1/9)) :} F=∫(((x^4 +x^2 +1)dx)/((x^2 +4)^2 (x^2 +1))) =∫(((8x^2 −7)/(9(x^2 +4)^2 ))+(1/(9(x^2 +1))))dx =(8/9)∫((((x^2 +4)−11)/((x^2 +4)^2 ))+(1/(9(x^2 +1))))dx =(8/9)∫(dx/(x^2 +4))−∫((88dx)/(9(x^2 +4)^2 ))+∫(dx/(9(x^2 +1))) =(4/9)tan^(−1) ((x/2))+(1/9)tan^(−1) (x)−((88)/9)A A=(1/(2.4)).(x/(x^2 +4))+(1/4).(1/2)∫(dx/(x^2 +4)) =(x/(8(x^2 +4)))+(1/8)×(1/2)tan^(−1) (x/2) F=(4/9)tan^(−1) ((x/2))+(1/9)tan^(−1) (x)−((88)/9)[ (1/8)((x/(x^2 +4))+(1/2)tan^(−1) ((x/2)))] =((−1)/6)tan^(−1) ((x/2))+(1/9)tan^(−1) (x) −((11)/9).(x/(x^2 +4))+C
$$\frac{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:=\frac{\mathrm{ax}^{\mathrm{3}} +\mathrm{bx}^{\mathrm{2}} +\mathrm{cx}+\mathrm{d}}{\mathrm{x}^{\mathrm{4}} +\mathrm{8x}^{\mathrm{2}} +\mathrm{16}}+\frac{\mathrm{ex}+\mathrm{f}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}=\left(\mathrm{a}+\mathrm{e}\right)\mathrm{x}^{\mathrm{5}} +\left(\mathrm{b}+\mathrm{f}\right)\mathrm{x}^{\mathrm{4}} +\left(\mathrm{a}+\mathrm{c}+\mathrm{8e}\right)\mathrm{x}^{\mathrm{3}} \\ $$$$+\left(\mathrm{b}+\mathrm{d}+\mathrm{8f}\right)\mathrm{x}^{\mathrm{2}} +\left(\mathrm{c}+\mathrm{16e}\right)\mathrm{x}+\mathrm{d}+\mathrm{16f} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{a}+\mathrm{e}=\mathrm{0}}\\{\mathrm{b}+\mathrm{f}=\mathrm{1}}\\{\mathrm{a}+\mathrm{c}+\mathrm{8e}=\mathrm{0}}\\{\mathrm{b}+\mathrm{d}+\mathrm{8f}=\mathrm{1}}\\{\mathrm{c}+\mathrm{16e}=\mathrm{0}}\\{\mathrm{d}+\mathrm{16f}=\mathrm{1}}\end{cases}\Leftrightarrow\begin{cases}{\mathrm{a}=\mathrm{c}=\mathrm{e}=\mathrm{0}}\\{\mathrm{b}=\mathrm{8}/\mathrm{9}}\\{\mathrm{d}=−\mathrm{7}/\mathrm{9}}\\{\mathrm{f}=\mathrm{1}/\mathrm{9}}\end{cases} \\ $$$$\mathrm{F}=\int\frac{\left({x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{dx}}{\left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:=\int\left(\frac{\mathrm{8x}^{\mathrm{2}} −\mathrm{7}}{\mathrm{9}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{9}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{8}}{\mathrm{9}}\int\left(\frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)−\mathrm{11}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{9}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{8}}{\mathrm{9}}\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{4}}−\int\frac{\mathrm{88dx}}{\mathrm{9}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} }+\int\frac{\mathrm{dx}}{\mathrm{9}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{4}}{\mathrm{9}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{9}}\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)−\frac{\mathrm{88}}{\mathrm{9}}\mathrm{A} \\ $$$$\mathrm{A}=\frac{\mathrm{1}}{\mathrm{2}.\mathrm{4}}.\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{4}} \\ $$$$=\frac{\mathrm{x}}{\mathrm{8}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)}+\frac{\mathrm{1}}{\mathrm{8}}×\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{x}}{\mathrm{2}} \\ $$$$\mathrm{F}=\frac{\mathrm{4}}{\mathrm{9}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{9}}\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)−\frac{\mathrm{88}}{\mathrm{9}}\left[\right. \\ $$$$\left.\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)\right] \\ $$$$=\frac{−\mathrm{1}}{\mathrm{6}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{9}}\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right) \\ $$$$−\frac{\mathrm{11}}{\mathrm{9}}.\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{4}}+\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *