Question Number 183101 by Mastermind last updated on 20/Dec/22

$$\int\frac{\mathrm{x}+\mathrm{4y}}{\mathrm{2x}^{\mathrm{2}} +\mathrm{9xy}}\mathrm{dx} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$
Commented by mr W last updated on 20/Dec/22

$${is}\:{y}\:{a}\:{constant}\:{or}\:{a}\:{function}\:{of}\:{x}? \\ $$
Commented by MJS_new last updated on 21/Dec/22

$$\mathrm{wrong}. \\ $$$$\mathrm{maybe}\:\mathrm{better}\:\mathrm{celebrate}\:{after}\:\mathrm{learning}\:\mathrm{the} \\ $$$$\mathrm{basics}?! \\ $$
Commented by mr W last updated on 21/Dec/22

$${even}\:{maybe}\:{better}\:{learn}\:{basic}\:{human} \\ $$$${behavior}\:{at}\:{first}\:{before}\:{leraning}\:{basic} \\ $$$${mathematics}! \\ $$$${i}\:{kindly}\:{asked}\:{him}\:{many}\:{times}\:{not}\: \\ $$$${to}\:{post}\:{answers}\:{as}\:“{comment}''\:{but}\:{as} \\ $$$$“{answer}'',\:{i}\:{even}\:{told}\:{him}\:{how}\:{to}\:{do} \\ $$$${this},\:{i}\:{even}\:{told}\:{him}\:{in}\:{his}\:{language} \\ $$$$\left({French}\right),\:{but}\:{he}\:{ignored}\:{all}\:{those}\: \\ $$$${kindnesses}\:{and}\:{even}\:{didn}'{t}\:{give}\:{any} \\ $$$${reply}.\:{therefore}\:{i}\:{would}\:{say}\:{what}\:{he}\: \\ $$$${mostly}\:{misses}\:{is}\:{the}\:{basic}\:{human}\: \\ $$$${behavior}. \\ $$
Answered by MJS_new last updated on 21/Dec/22
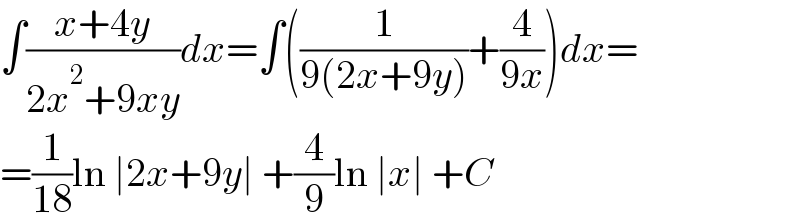
$$\int\frac{{x}+\mathrm{4}{y}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{9}{xy}}{dx}=\int\left(\frac{\mathrm{1}}{\mathrm{9}\left(\mathrm{2}{x}+\mathrm{9}{y}\right)}+\frac{\mathrm{4}}{\mathrm{9}{x}}\right){dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{18}}\mathrm{ln}\:\mid\mathrm{2}{x}+\mathrm{9}{y}\mid\:+\frac{\mathrm{4}}{\mathrm{9}}\mathrm{ln}\:\mid{x}\mid\:+{C} \\ $$
