Question Number 16061 by Joel577 last updated on 17/Jun/17
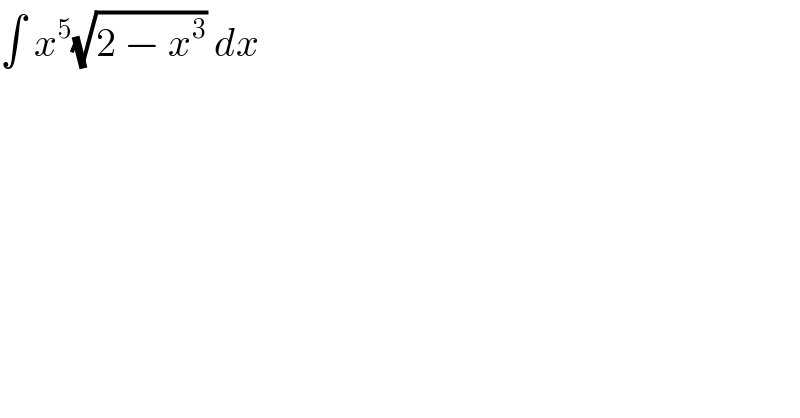
$$\int\:{x}^{\mathrm{5}} \sqrt{\mathrm{2}\:−\:{x}^{\mathrm{3}} }\:{dx} \\ $$
Answered by Tinkutara last updated on 17/Jun/17
![Let 2 − x^3 = t Then −3x^2 dx = dt ∴ ((−1)/3) ∫x^3 [−3x^2 (√(2 − x^3 )) dx] = (1/3) ∫(t − 2)(√t) dt = (1/3) ∫[(√t^3 ) − 2(√t)] dt Now simply integrate and substitute for t.](https://www.tinkutara.com/question/Q16062.png)
$$\mathrm{Let}\:\mathrm{2}\:−\:{x}^{\mathrm{3}} \:=\:{t} \\ $$$$\mathrm{Then}\:−\mathrm{3}{x}^{\mathrm{2}} \:{dx}\:=\:{dt} \\ $$$$\therefore\:\frac{−\mathrm{1}}{\mathrm{3}}\:\int{x}^{\mathrm{3}} \:\left[−\mathrm{3}{x}^{\mathrm{2}} \:\sqrt{\mathrm{2}\:−\:{x}^{\mathrm{3}} }\:{dx}\right] \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{3}}\:\int\left({t}\:−\:\mathrm{2}\right)\sqrt{{t}}\:{dt} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{3}}\:\int\left[\sqrt{{t}^{\mathrm{3}} }\:−\:\mathrm{2}\sqrt{{t}}\right]\:{dt} \\ $$$$\mathrm{Now}\:\mathrm{simply}\:\mathrm{integrate}\:\mathrm{and}\:\mathrm{substitute} \\ $$$$\mathrm{for}\:{t}. \\ $$
Commented by Joel577 last updated on 18/Jun/17
$${thank}\:{you}\:{very}\:{much} \\ $$
