Menu Close

x-5-3x-4-23x-3-51x-2-94x-120-8x-3-42-x-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 37425 by MJS last updated on 13/Jun/18
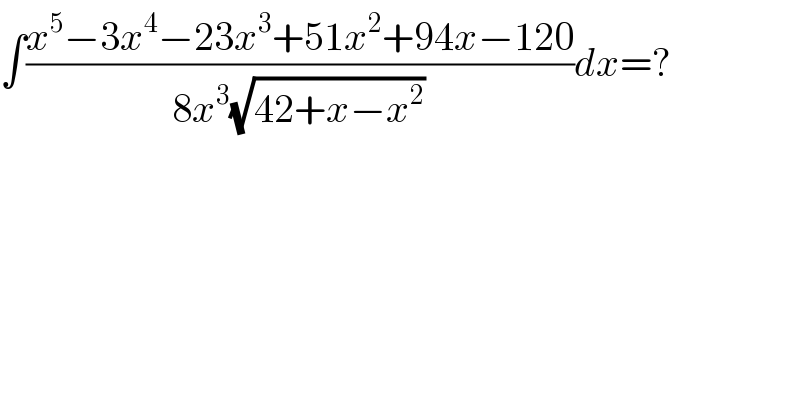
∫((x^5 −3x^4 −23x^3 +51x^2 +94x−120)/(8x^3 (√(42+x−x^2 ))))dx=?
$$\int\frac{{x}^{\mathrm{5}} −\mathrm{3}{x}^{\mathrm{4}} −\mathrm{23}{x}^{\mathrm{3}} +\mathrm{51}{x}^{\mathrm{2}} +\mathrm{94}{x}−\mathrm{120}}{\mathrm{8}{x}^{\mathrm{3}} \sqrt{\mathrm{42}+{x}−{x}^{\mathrm{2}} }}{dx}=? \\ $$
Answered by ajfour last updated on 13/Jun/18
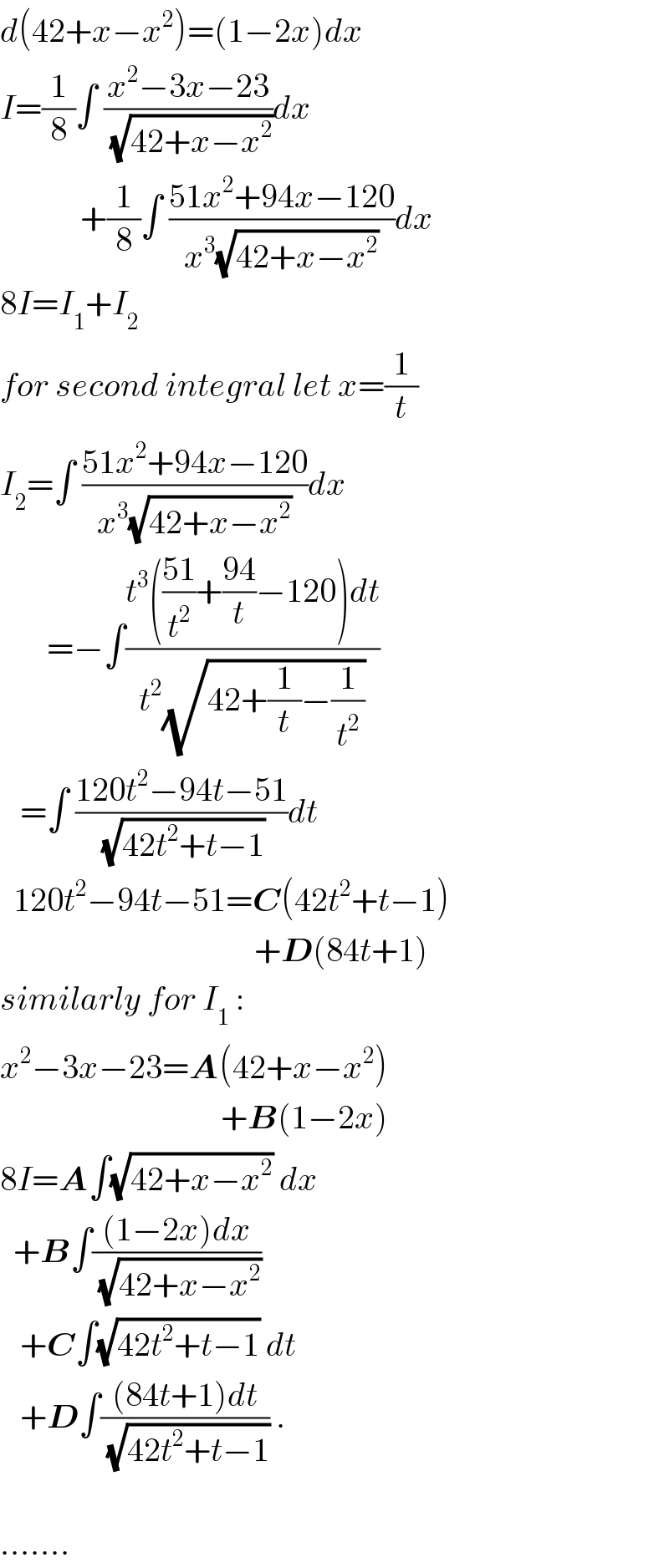
d(42+x−x^2 )=(1−2x)dx I=(1/8)∫ ((x^2 −3x−23)/( (√(42+x−x^2 ))))dx +(1/8)∫ ((51x^2 +94x−120)/(x^3 (√(42+x−x^2 ))))dx 8I=I_1 +I_2 for second integral let x=(1/t) I_2 =∫ ((51x^2 +94x−120)/(x^3 (√(42+x−x^2 ))))dx =−∫((t^3 (((51)/t^2 )+((94)/t)−120)dt)/(t^2 (√(42+(1/t)−(1/t^2 ))))) =∫ ((120t^2 −94t−51)/( (√(42t^2 +t−1))))dt 120t^2 −94t−51=C(42t^2 +t−1) +D(84t+1) similarly for I_1 : x^2 −3x−23=A(42+x−x^2 ) +B(1−2x) 8I=A∫(√(42+x−x^2 )) dx +B∫(((1−2x)dx)/( (√(42+x−x^2 )))) +C∫(√(42t^2 +t−1)) dt +D∫(((84t+1)dt)/( (√(42t^2 +t−1)))) . .......
$${d}\left(\mathrm{42}+{x}−{x}^{\mathrm{2}} \right)=\left(\mathrm{1}−\mathrm{2}{x}\right){dx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{8}}\int\:\frac{{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{23}}{\:\sqrt{\mathrm{42}+{x}−{x}^{\mathrm{2}} }}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{8}}\int\:\frac{\mathrm{51}{x}^{\mathrm{2}} +\mathrm{94}{x}−\mathrm{120}}{{x}^{\mathrm{3}} \sqrt{\mathrm{42}+{x}−{x}^{\mathrm{2}} }}{dx} \\ $$$$\mathrm{8}{I}={I}_{\mathrm{1}} +{I}_{\mathrm{2}} \\ $$$${for}\:{second}\:{integral}\:{let}\:{x}=\frac{\mathrm{1}}{{t}} \\ $$$${I}_{\mathrm{2}} =\int\:\frac{\mathrm{51}{x}^{\mathrm{2}} +\mathrm{94}{x}−\mathrm{120}}{{x}^{\mathrm{3}} \sqrt{\mathrm{42}+{x}−{x}^{\mathrm{2}} }}{dx}\: \\ $$$$\:\:\:\:\:\:\:=−\int\frac{{t}^{\mathrm{3}} \left(\frac{\mathrm{51}}{{t}^{\mathrm{2}} }+\frac{\mathrm{94}}{{t}}−\mathrm{120}\right){dt}}{{t}^{\mathrm{2}} \sqrt{\mathrm{42}+\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}} \\ $$$$\:\:\:=\int\:\frac{\mathrm{120}{t}^{\mathrm{2}} −\mathrm{94}{t}−\mathrm{51}}{\:\sqrt{\mathrm{42}{t}^{\mathrm{2}} +{t}−\mathrm{1}}}{dt}\:\: \\ $$$$\:\:\mathrm{120}{t}^{\mathrm{2}} −\mathrm{94}{t}−\mathrm{51}=\boldsymbol{{C}}\left(\mathrm{42}{t}^{\mathrm{2}} +{t}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\boldsymbol{{D}}\left(\mathrm{84}{t}+\mathrm{1}\right) \\ $$$${similarly}\:{for}\:{I}_{\mathrm{1}} \:: \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{23}=\boldsymbol{{A}}\left(\mathrm{42}+{x}−{x}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\boldsymbol{{B}}\left(\mathrm{1}−\mathrm{2}{x}\right) \\ $$$$\mathrm{8}{I}=\boldsymbol{{A}}\int\sqrt{\mathrm{42}+{x}−{x}^{\mathrm{2}} }\:{dx} \\ $$$$\:\:+\boldsymbol{{B}}\int\frac{\left(\mathrm{1}−\mathrm{2}{x}\right){dx}}{\:\sqrt{\mathrm{42}+{x}−{x}^{\mathrm{2}} }}\: \\ $$$$\:\:\:+\boldsymbol{{C}}\int\sqrt{\mathrm{42}{t}^{\mathrm{2}} +{t}−\mathrm{1}}\:{dt} \\ $$$$\:\:\:+\boldsymbol{{D}}\int\frac{\left(\mathrm{84}{t}+\mathrm{1}\right){dt}}{\:\sqrt{\mathrm{42}{t}^{\mathrm{2}} +{t}−\mathrm{1}}}\:. \\ $$$$ \\ $$$$……. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *