Question Number 55198 by ajfour last updated on 19/Feb/19
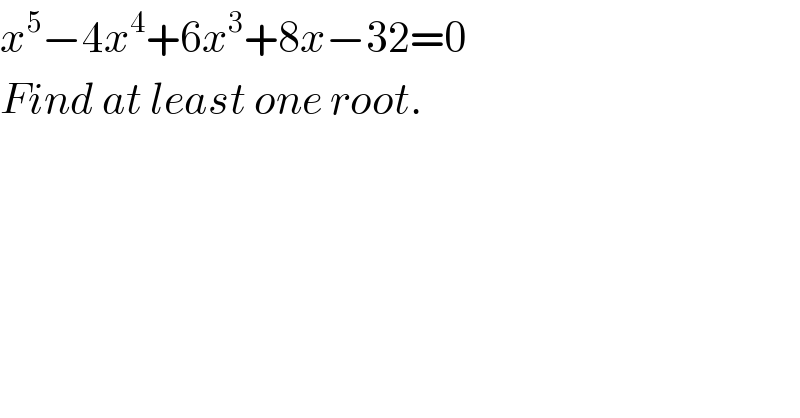
$${x}^{\mathrm{5}} −\mathrm{4}{x}^{\mathrm{4}} +\mathrm{6}{x}^{\mathrm{3}} +\mathrm{8}{x}−\mathrm{32}=\mathrm{0} \\ $$$${Find}\:{at}\:{least}\:{one}\:{root}. \\ $$
Commented by arvinddayama00@gmail.com last updated on 19/Feb/19

$${all}\:{velue}\:{of}\:{x}=? \\ $$
Answered by rahul 19 last updated on 19/Feb/19

$${x}=\mathrm{2}! \\ $$
Commented by rahul 19 last updated on 19/Feb/19
simply by hit & trial . ����
Answered by tanmay.chaudhury50@gmail.com last updated on 19/Feb/19

$${x}^{\mathrm{5}} +\mathrm{6}{x}^{\mathrm{3}} +\mathrm{8}{x}=\mathrm{4}{x}^{\mathrm{4}} +\mathrm{32} \\ $$$${right}\:{hand}\:{side}\:{x}^{{even}\:{power}} \:{so}\:{right}\:{hand} \\ $$$${side}\:{is}\:{always}\:+{ve} \\ $$$${now}\:{left}\:{hand}\:{side}\:{should}\:{be}\:+{ve} \\ $$$${so}\:{x}\:{can}\:{not}\:{be}\:{less}\:{than}\:{zero} \\ $$$${so}\:{x}\nless\mathrm{0} \\ $$$${now}\:\: \\ $$$$\left({x}^{\mathrm{5}} +\mathrm{6}{x}^{\mathrm{3}} +\mathrm{8}{x}\right)−\left(\mathrm{4}{x}^{\mathrm{4}} +\mathrm{32}\right)=\mathrm{0} \\ $$$${f}\left({x}\right)=\left({x}^{\mathrm{5}} +\mathrm{6}{x}^{\mathrm{3}} +\mathrm{8}{x}\right)−\left(\mathrm{4}{x}^{\mathrm{4}} +\mathrm{32}\right) \\ $$$${f}\left({x}\right)<\mathrm{0}\:{at}\:{x}=\mathrm{0} \\ $$$${f}\left({x}\right)<\mathrm{0}\:{at}\:{x}=\mathrm{1} \\ $$$${so}\:{no}\:{root}\:{in}\:{between}\left(\mathrm{0},\mathrm{1}\right) \\ $$$$ \\ $$$${now}\:{checking}\:\:{between}\:\mathrm{1}\:{and}\:\mathrm{2} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{32}+\mathrm{48}+\mathrm{16}−\mathrm{64}−\mathrm{32}=\mathrm{0} \\ $$$${so}\:{x}=\mathrm{2}\:{is}\:{a}\:{root}.. \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1}+\mathrm{6}+\mathrm{8}−\mathrm{4}−\mathrm{32}=−\mathrm{21} \\ $$$${now}\:{gradually}\:{we}\:{increase}\:{the}\:{value}\:{of}\:{x} \\ $$$${such}\:{as}\:\mathrm{1}.\mathrm{1},\mathrm{1}.\mathrm{2},…{and}\:{observe}\:{change}\:{of}\:{sign} \\ $$$${f}\left({x}\right)={y}=\left({x}^{\mathrm{5}} +\mathrm{6}{x}^{\mathrm{3}} +\mathrm{8}{x}\right)−\left(\mathrm{4}{x}^{\mathrm{4}} +\mathrm{32}\right) \\ $$$$\frac{{dy}}{{dx}}=\mathrm{5}{x}^{\mathrm{4}} +\mathrm{18}{x}^{\mathrm{2}} +\mathrm{8}−\mathrm{16}{x}^{\mathrm{3}} \\ $$$$\frac{\bigtriangleup{y}}{\bigtriangleup{x}}\approx\frac{{dy}}{{dx}} \\ $$$$\bigtriangleup{y}=\frac{{dy}}{{dx}}×\bigtriangleup{x}=\left(\mathrm{5}+\mathrm{18}+\mathrm{8}−\mathrm{16}\right)×\mathrm{0}.\mathrm{1}=\mathrm{1}.\mathrm{5} \\ $$$${so}\:{f}\left(\mathrm{1}.\mathrm{1}\right)={f}\left(\mathrm{1}\right)+\bigtriangleup{y}=−\mathrm{21}+\mathrm{1}.\mathrm{5}=−\mathrm{19}.\mathrm{5} \\ $$$${f}\left(\mathrm{2}.\mathrm{1}\right)={f}\left(\mathrm{2}\right)+\bigtriangleup{y}=\mathrm{0}+\mathrm{1}.\mathrm{5}=\mathrm{1}.\mathrm{5}>\mathrm{0} \\ $$$${f}\left(\mathrm{3}\right)=\mathrm{3}^{\mathrm{5}} +\mathrm{6}×\mathrm{3}^{\mathrm{3}} +\mathrm{8}×\mathrm{3}−\mathrm{4}×\mathrm{3}^{\mathrm{4}} −\mathrm{32} \\ $$$$=\mathrm{3}^{\mathrm{4}} \left(\mathrm{3}−\mathrm{4}\right)+\mathrm{6}×\mathrm{27}−\mathrm{8} \\ $$$$=−\mathrm{81}+\mathrm{162}−\mathrm{8}>\mathrm{0} \\ $$$${so}\:{no}\:{root}\:{between}\:\mathrm{2}.\mathrm{1}\:{and}\:\mathrm{3} \\ $$$$… \\ $$$${f}\left(\mathrm{4}\right)=\mathrm{4}^{\mathrm{5}} +\mathrm{6}×\mathrm{4}^{\mathrm{3}} +\mathrm{32}−\mathrm{4}×\mathrm{4}^{\mathrm{4}} −\mathrm{32}>\mathrm{0} \\ $$$${so}\:{no}\:{root}\:{between}\:\mathrm{3}\:{and}\:\mathrm{4} \\ $$$${now}… \\ $$$${f}\left({x}\right)={x}^{\mathrm{5}} +\mathrm{6}{x}^{\mathrm{3}} +\mathrm{8}{x}−\left(\mathrm{4}{x}^{\mathrm{4}} +\mathrm{32}\right) \\ $$$${f}\left({x}\right)={g}\left({x}\right)−{h}\left({x}\right) \\ $$$$\frac{{df}}{{dx}}=\frac{{dg}}{{dx}}−\frac{{dh}}{{dx}}=\left(\mathrm{5}{x}^{\mathrm{4}} +\mathrm{18}{x}^{\mathrm{2}} +\mathrm{8}\right)−\left(\mathrm{16}{x}^{\mathrm{3}} \right) \\ $$$$={x}^{\mathrm{3}} \left(\mathrm{5}{x}−\mathrm{16}\right)+\mathrm{18}{x}^{\mathrm{2}} +\mathrm{8}.. \\ $$$${now}\:{look}\:{when}\:{x}>\mathrm{3}.\mathrm{2}\:\:\:\:\frac{{df}}{{dx}}>\mathrm{0} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{there}}\:\boldsymbol{{will}}\:\boldsymbol{{be}}\:\boldsymbol{{no}}\:\boldsymbol{{sign}}\:\boldsymbol{{change}}\:\boldsymbol{{when}}\:\boldsymbol{{x}}>\mathrm{3}.\mathrm{2} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{this}}\:\boldsymbol{{eqn}}\:\boldsymbol{{has}}\:\boldsymbol{{only}}\:\boldsymbol{{one}}\:\boldsymbol{{root}}\:\boldsymbol{{that}}\:\boldsymbol{{is}} \\ $$$$\boldsymbol{{x}}=\mathrm{2}…\boldsymbol{{pls}}\:\boldsymbol{{pay}}\:\boldsymbol{{your}}\:\boldsymbol{{kind}}\:\boldsymbol{{attention}}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
