Question Number 148408 by cesarL last updated on 27/Jul/21

$$\int{x}^{\mathrm{5}} {e}^{{x}^{\mathrm{2}} } {dx} \\ $$$${Help}\:{please}! \\ $$
Answered by Olaf_Thorendsen last updated on 27/Jul/21
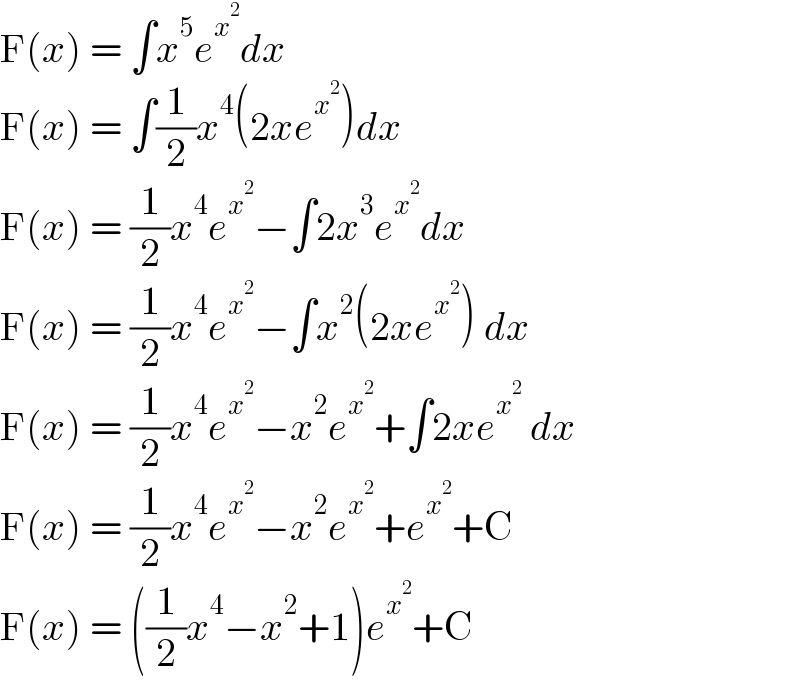
$$\mathrm{F}\left({x}\right)\:=\:\int{x}^{\mathrm{5}} {e}^{{x}^{\mathrm{2}} } {dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\int\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{4}} \left(\mathrm{2}{xe}^{{x}^{\mathrm{2}} } \right){dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{4}} {e}^{{x}^{\mathrm{2}} } −\int\mathrm{2}{x}^{\mathrm{3}} {e}^{{x}^{\mathrm{2}} } {dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{4}} {e}^{{x}^{\mathrm{2}} } −\int{x}^{\mathrm{2}} \left(\mathrm{2}{xe}^{{x}^{\mathrm{2}} } \right)\:{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{4}} {e}^{{x}^{\mathrm{2}} } −{x}^{\mathrm{2}} {e}^{{x}^{\mathrm{2}} } +\int\mathrm{2}{xe}^{{x}^{\mathrm{2}} } \:{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{4}} {e}^{{x}^{\mathrm{2}} } −{x}^{\mathrm{2}} {e}^{{x}^{\mathrm{2}} } +{e}^{{x}^{\mathrm{2}} } +\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\left(\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right){e}^{{x}^{\mathrm{2}} } +\mathrm{C} \\ $$
Commented by cesarL last updated on 27/Jul/21

$${thank}\:{u}\:{sir} \\ $$
Answered by Math_Freak last updated on 27/Jul/21

$$\int\left({x}^{\mathrm{2}} \right)^{\mathrm{2}} {xe}^{{x}^{\mathrm{2}} } {dx} \\ $$$${let}\:{u}\:=\:{x}^{\mathrm{2}} \\ $$$${dx}\:=\:\frac{{du}}{\mathrm{2}{x}} \\ $$$$\int{u}^{\mathrm{2}} {xe}^{{u}} \bullet\frac{{du}}{\mathrm{2}{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int{u}^{\mathrm{2}} {e}^{{u}} \:{du} \\ $$$${integrating}\:{by}\:{parts} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({u}^{\mathrm{2}} {e}^{{u}} \:−\:\mathrm{2}\int{ue}^{{u}} \:{du}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({u}^{\mathrm{2}} {e}^{{u}} \:−\:\mathrm{2}\left({ue}^{{u}} \:−\:\int{e}^{{u}} \:{du}\right)\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({u}^{\mathrm{2}} {e}^{{u}} \:−\:\mathrm{2}\left({ue}^{{u}} \:−\:{e}^{{u}} \right)\right)\:+\:{C} \\ $$$$\frac{{u}^{\mathrm{2}} {e}^{{u}} }{\mathrm{2}}\:−\:{ue}^{{u}} \:+\:{e}^{{u}} \:+\:{C} \\ $$$${u}\:=\:{x}^{\mathrm{2}} \\ $$$$\frac{{x}^{\mathrm{4}} {e}^{{x}^{\mathrm{2}} } }{\mathrm{2}}\:−\:{x}^{\mathrm{2}} {e}^{{x}^{\mathrm{2}} } \:+\:{e}^{{x}^{\mathrm{2}} } \:+\:{C} \\ $$
