Question Number 124101 by Ar Brandon last updated on 30/Nov/20
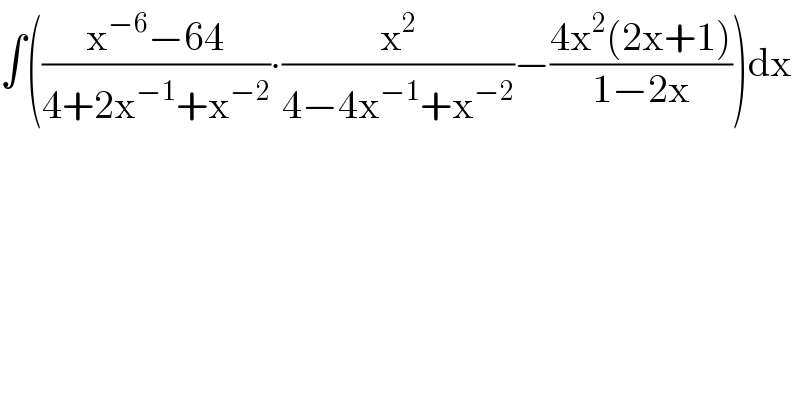
$$\int\left(\frac{\mathrm{x}^{−\mathrm{6}} −\mathrm{64}}{\mathrm{4}+\mathrm{2x}^{−\mathrm{1}} +\mathrm{x}^{−\mathrm{2}} }\centerdot\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}−\mathrm{4x}^{−\mathrm{1}} +\mathrm{x}^{−\mathrm{2}} }−\frac{\mathrm{4x}^{\mathrm{2}} \left(\mathrm{2x}+\mathrm{1}\right)}{\mathrm{1}−\mathrm{2x}}\right)\mathrm{dx} \\ $$
Answered by MJS_new last updated on 30/Nov/20
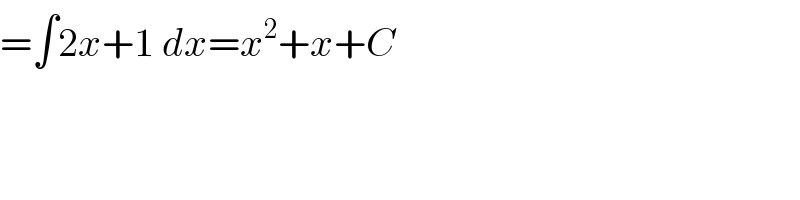
$$=\int\mathrm{2}{x}+\mathrm{1}\:{dx}={x}^{\mathrm{2}} +{x}+{C} \\ $$
Commented by Ar Brandon last updated on 30/Nov/20
����
