Question Number 40684 by vajpaithegrate@gmail.com last updated on 26/Jul/18

$$\int\frac{\mathrm{x}^{\mathrm{7}} −\mathrm{1}}{\mathrm{logx}}\mathrm{dx} \\ $$
Commented by math khazana by abdo last updated on 26/Jul/18
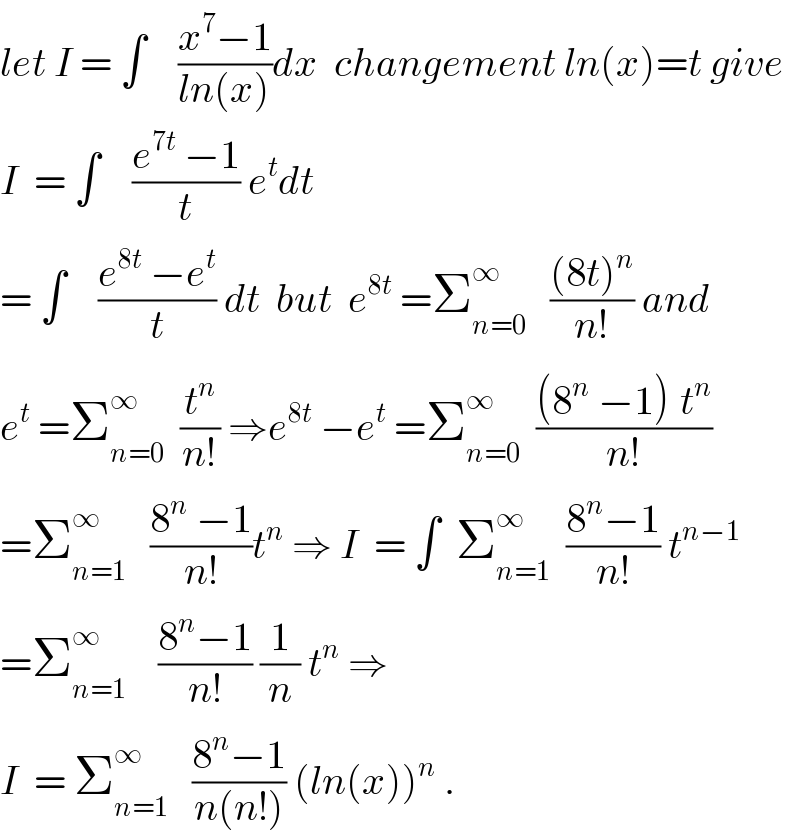
$${let}\:{I}\:=\:\int\:\:\:\:\frac{{x}^{\mathrm{7}} −\mathrm{1}}{{ln}\left({x}\right)}{dx}\:\:{changement}\:{ln}\left({x}\right)={t}\:{give} \\ $$$${I}\:\:=\:\int\:\:\:\:\frac{{e}^{\mathrm{7}{t}} \:−\mathrm{1}}{{t}}\:{e}^{{t}} {dt} \\ $$$$=\:\int\:\:\:\:\frac{{e}^{\mathrm{8}{t}} \:−{e}^{{t}} }{{t}}\:{dt}\:\:{but}\:\:{e}^{\mathrm{8}{t}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\left(\mathrm{8}{t}\right)^{{n}} }{{n}!}\:{and} \\ $$$${e}^{{t}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{t}^{{n}} }{{n}!}\:\Rightarrow{e}^{\mathrm{8}{t}} \:−{e}^{{t}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(\mathrm{8}^{{n}} \:−\mathrm{1}\right)^{} {t}^{{n}} }{{n}!} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{8}^{{n}} \:−\mathrm{1}}{{n}!}{t}^{{n}} \:\Rightarrow\:{I}\:\:=\:\int\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{8}^{{n}} −\mathrm{1}}{{n}!}\:{t}^{{n}−\mathrm{1}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\:\frac{\mathrm{8}^{{n}} −\mathrm{1}}{{n}!}\:\frac{\mathrm{1}}{{n}}\:{t}^{{n}} \:\Rightarrow \\ $$$${I}\:\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{8}^{{n}} −\mathrm{1}}{{n}\left({n}!\right)}\:\left({ln}\left({x}\right)\right)^{{n}} \:. \\ $$
