Question Number 125542 by TITA last updated on 11/Dec/20
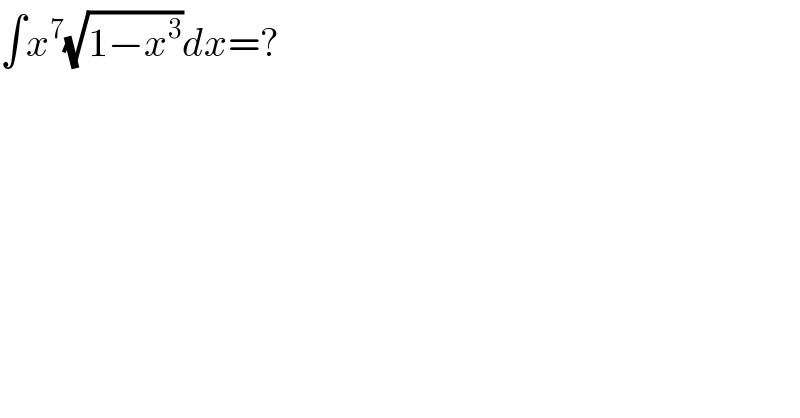
$$\int{x}^{\mathrm{7}} \sqrt{\mathrm{1}−{x}^{\mathrm{3}} }{dx}=? \\ $$
Commented by TITA last updated on 11/Dec/20

$${please}\:{help} \\ $$
Answered by mathmax by abdo last updated on 12/Dec/20
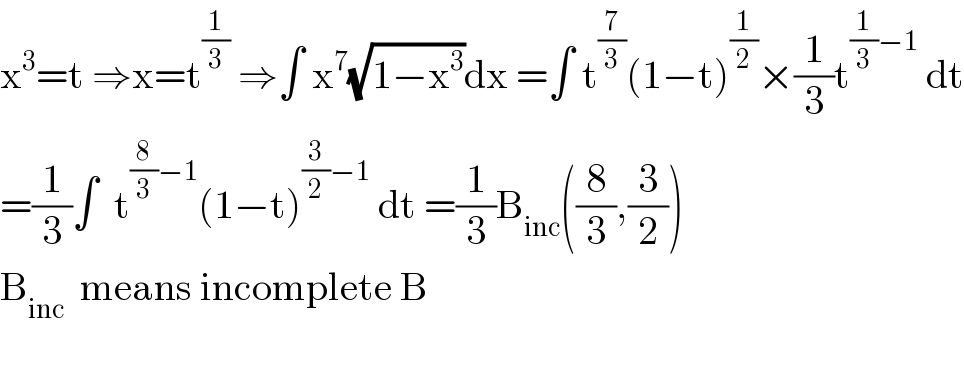
$$\mathrm{x}^{\mathrm{3}} =\mathrm{t}\:\Rightarrow\mathrm{x}=\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{3}}} \:\Rightarrow\int\:\mathrm{x}^{\mathrm{7}} \sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{3}} }\mathrm{dx}\:=\int\:\mathrm{t}^{\frac{\mathrm{7}}{\mathrm{3}}} \left(\mathrm{1}−\mathrm{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} ×\frac{\mathrm{1}}{\mathrm{3}}\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int\:\:\mathrm{t}^{\frac{\mathrm{8}}{\mathrm{3}}−\mathrm{1}} \left(\mathrm{1}−\mathrm{t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}} \:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{B}_{\mathrm{inc}} \left(\frac{\mathrm{8}}{\mathrm{3}},\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$\mathrm{B}_{\mathrm{inc}} \:\:\mathrm{means}\:\mathrm{incomplete}\:\mathrm{B} \\ $$$$ \\ $$
