Question Number 129787 by EDWIN88 last updated on 19/Jan/21
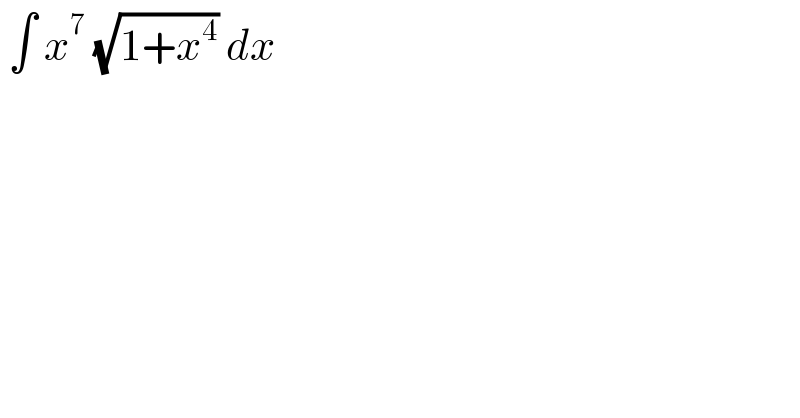
$$\:\int\:{x}^{\mathrm{7}} \:\sqrt{\mathrm{1}+{x}^{\mathrm{4}} }\:{dx}\: \\ $$
Answered by bramlexs22 last updated on 19/Jan/21

Commented by MJS_new last updated on 19/Jan/21
![∫x^7 (√(x^4 +1)) dx= [w=(√(x^4 +1)) → dx=((√(x^4 +1))/(2x^3 ))dw] =(1/2)∫(w^4 −w^2 )dw=(w^5 /(10))−(w^3 /6)=(1/(30))w^3 (3w^2 −5)= =(((x^4 +1)^(3/2) (3x^4 −2))/(30))+C (=(1/(30))(3x^8 +x^4 −2)(√(x^4 +1))+C)](https://www.tinkutara.com/question/Q129799.png)
$$\int{x}^{\mathrm{7}} \sqrt{{x}^{\mathrm{4}} +\mathrm{1}}\:{dx}= \\ $$$$\:\:\:\:\:\left[{w}=\sqrt{{x}^{\mathrm{4}} +\mathrm{1}}\:\rightarrow\:{dx}=\frac{\sqrt{{x}^{\mathrm{4}} +\mathrm{1}}}{\mathrm{2}{x}^{\mathrm{3}} }{dw}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left({w}^{\mathrm{4}} −{w}^{\mathrm{2}} \right){dw}=\frac{{w}^{\mathrm{5}} }{\mathrm{10}}−\frac{{w}^{\mathrm{3}} }{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{30}}{w}^{\mathrm{3}} \left(\mathrm{3}{w}^{\mathrm{2}} −\mathrm{5}\right)= \\ $$$$=\frac{\left({x}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} \left(\mathrm{3}{x}^{\mathrm{4}} −\mathrm{2}\right)}{\mathrm{30}}+{C} \\ $$$$\left(=\frac{\mathrm{1}}{\mathrm{30}}\left(\mathrm{3}{x}^{\mathrm{8}} +{x}^{\mathrm{4}} −\mathrm{2}\right)\sqrt{{x}^{\mathrm{4}} +\mathrm{1}}+{C}\right) \\ $$
