Question Number 27525 by sirigidiravikumar@gmail.com last updated on 08/Jan/18
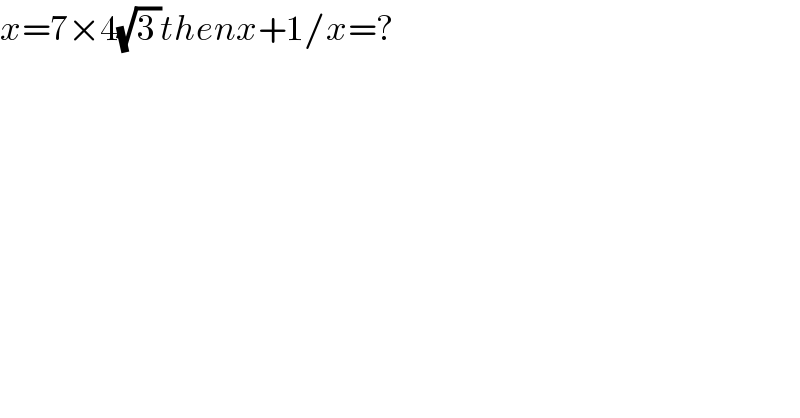
$${x}=\mathrm{7}×\mathrm{4}\sqrt{\mathrm{3}\:}{thenx}+\mathrm{1}/{x}=? \\ $$
Commented by Rasheed.Sindhi last updated on 09/Jan/18
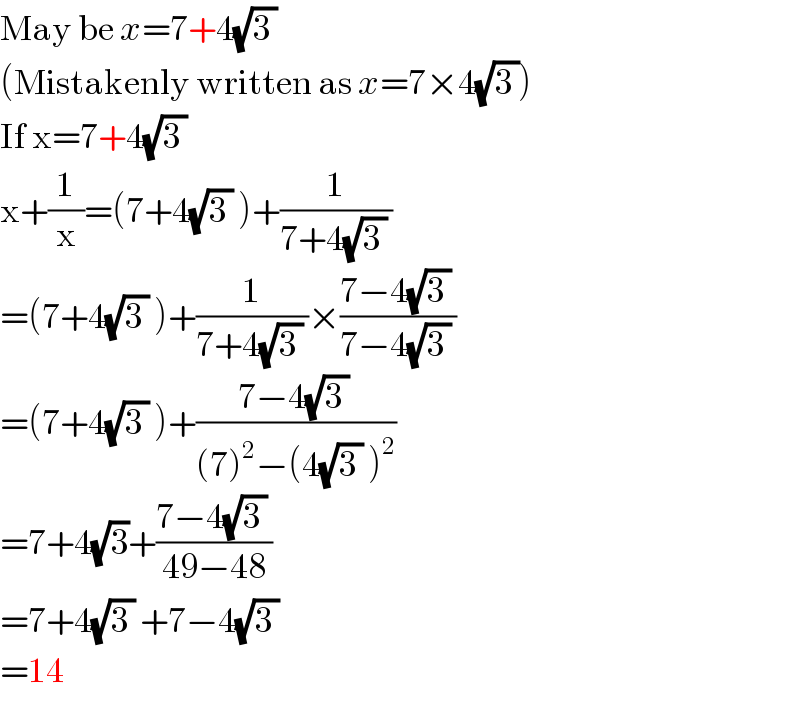
$$\mathrm{May}\:\mathrm{be}\:{x}=\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}\:}\:\:\: \\ $$$$\left(\mathrm{Mistakenly}\:\mathrm{written}\:\mathrm{as}\:{x}=\mathrm{7}×\mathrm{4}\sqrt{\mathrm{3}\:}\right) \\ $$$$\mathrm{If}\:\mathrm{x}=\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}\:}\: \\ $$$$\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}=\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}\:}\:\right)+\frac{\mathrm{1}}{\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}\:}\:} \\ $$$$=\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}\:}\:\right)+\frac{\mathrm{1}}{\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}\:}\:}×\frac{\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}\:}\:}{\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}\:}\:} \\ $$$$=\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}\:}\:\right)+\frac{\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}\:}\:}{\left(\mathrm{7}\right)^{\mathrm{2}} −\left(\mathrm{4}\sqrt{\mathrm{3}\:}\:\right)^{\mathrm{2}} } \\ $$$$=\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}+\frac{\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}\:}\:}{\mathrm{49}−\mathrm{48}} \\ $$$$=\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}\:}\:+\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}\:}\: \\ $$$$=\mathrm{14} \\ $$
Answered by Joel578 last updated on 09/Jan/18
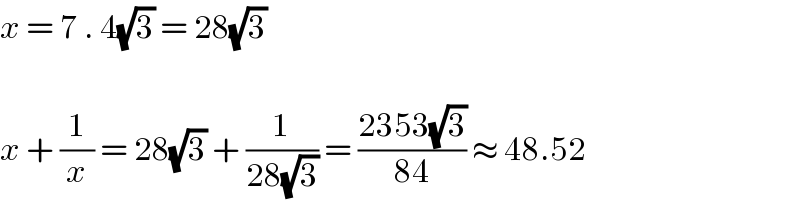
$${x}\:=\:\mathrm{7}\:.\:\mathrm{4}\sqrt{\mathrm{3}}\:=\:\mathrm{28}\sqrt{\mathrm{3}} \\ $$$$ \\ $$$${x}\:+\:\frac{\mathrm{1}}{{x}}\:=\:\mathrm{28}\sqrt{\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{28}\sqrt{\mathrm{3}}}\:=\:\frac{\mathrm{2353}\sqrt{\mathrm{3}}}{\mathrm{84}}\:\approx\:\mathrm{48}.\mathrm{52} \\ $$
