Question Number 87371 by M±th+et£s last updated on 04/Apr/20
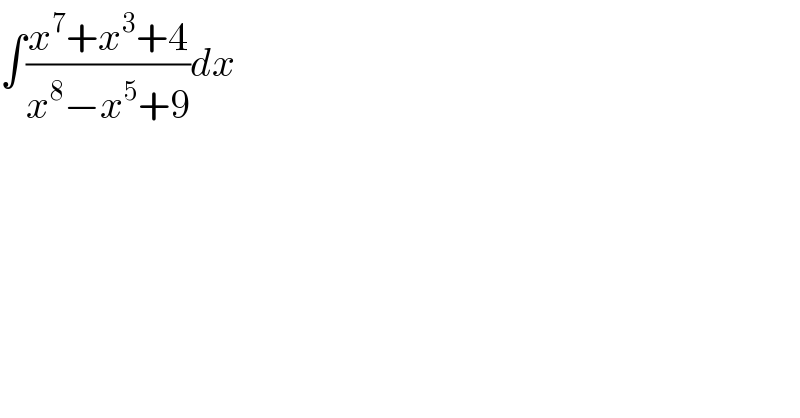
$$\int\frac{{x}^{\mathrm{7}} +{x}^{\mathrm{3}} +\mathrm{4}}{{x}^{\mathrm{8}} −{x}^{\mathrm{5}} +\mathrm{9}}{dx} \\ $$
Commented by M±th+et£s last updated on 04/Apr/20

$${why}\:{sir} \\ $$
Commented by MJS last updated on 04/Apr/20
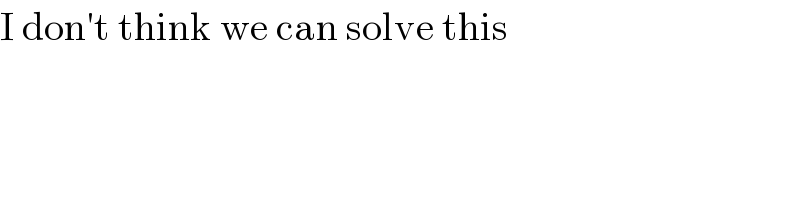
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{this} \\ $$
Commented by MJS last updated on 04/Apr/20
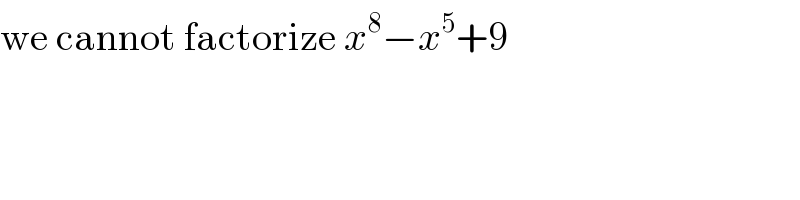
$$\mathrm{we}\:\mathrm{cannot}\:\mathrm{factorize}\:{x}^{\mathrm{8}} −{x}^{\mathrm{5}} +\mathrm{9} \\ $$
Answered by mind is power last updated on 04/Apr/20
![((x^7 +x^3 +4)/(x^8 −x^5 +9))=Σ_([w:w^8 −w^5 +9=0]) .((w^7 +w^3 +4)/((8w^7 −5w^4 )(x−w))) ∫((x^7 +x^3 +4)/(x^8 −x^5 +9))dx=Σ_([w:w^8 −w^5 +9=0]) ∫((w^7 +w^3 +4)/((8w^7 −5w^4 )(x−w)))dx Σ_([w:w^8 −w^5 +9]) ((w^7 +w^3 +4)/((8w^7 −5w^4 )))ln(x−w)+c](https://www.tinkutara.com/question/Q87491.png)
$$\frac{{x}^{\mathrm{7}} +{x}^{\mathrm{3}} +\mathrm{4}}{{x}^{\mathrm{8}} −{x}^{\mathrm{5}} +\mathrm{9}}=\underset{\left[{w}:{w}^{\mathrm{8}} −{w}^{\mathrm{5}} +\mathrm{9}=\mathrm{0}\right]} {\sum}.\frac{{w}^{\mathrm{7}} +{w}^{\mathrm{3}} +\mathrm{4}}{\left(\mathrm{8}{w}^{\mathrm{7}} −\mathrm{5}{w}^{\mathrm{4}} \right)\left({x}−{w}\right)} \\ $$$$\int\frac{{x}^{\mathrm{7}} +{x}^{\mathrm{3}} +\mathrm{4}}{{x}^{\mathrm{8}} −{x}^{\mathrm{5}} +\mathrm{9}}{dx}=\underset{\left[{w}:{w}^{\mathrm{8}} −{w}^{\mathrm{5}} +\mathrm{9}=\mathrm{0}\right]} {\sum}\int\frac{{w}^{\mathrm{7}} +{w}^{\mathrm{3}} +\mathrm{4}}{\left(\mathrm{8}{w}^{\mathrm{7}} −\mathrm{5}{w}^{\mathrm{4}} \right)\left({x}−{w}\right)}{dx} \\ $$$$\:\:\underset{\left[{w}:{w}^{\mathrm{8}} −{w}^{\mathrm{5}} +\mathrm{9}\right]} {\sum}\frac{{w}^{\mathrm{7}} +{w}^{\mathrm{3}} +\mathrm{4}}{\left(\mathrm{8}{w}^{\mathrm{7}} −\mathrm{5}{w}^{\mathrm{4}} \right)}{ln}\left({x}−{w}\right)+{c} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by MJS last updated on 04/Apr/20

$$\mathrm{yes},\:\mathrm{I}\:\mathrm{also}\:\mathrm{found}\:\mathrm{this},\:\mathrm{but}\:\mathrm{I}\:\mathrm{thought}\:\mathrm{it}\:\mathrm{was} \\ $$$$\mathrm{not}\:\mathrm{a}\:“\mathrm{solution}''… \\ $$
Commented by mind is power last updated on 04/Apr/20

$${realy}\:{is}\:{not}\:{a}\:{clear}\:{Solution} \\ $$
Commented by M±th+et£s last updated on 04/Apr/20

$${god}\:{bless}\:{you}\:{sir} \\ $$
