Question Number 164650 by cortano1 last updated on 20/Jan/22
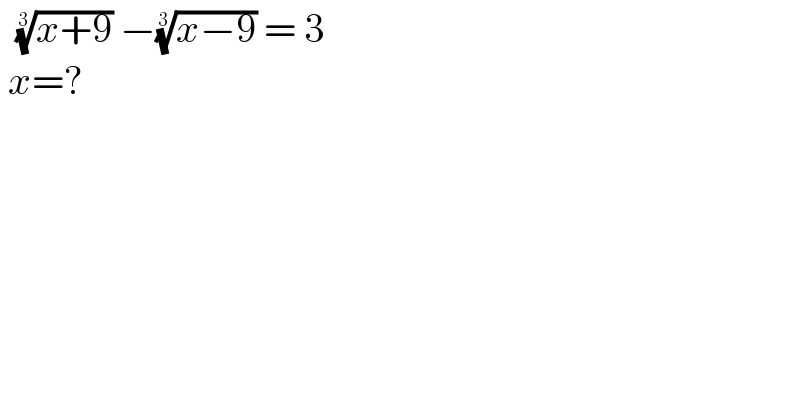
$$\:\:\sqrt[{\mathrm{3}}]{{x}+\mathrm{9}}\:−\sqrt[{\mathrm{3}}]{{x}−\mathrm{9}}\:=\:\mathrm{3}\: \\ $$$$\:{x}=? \\ $$
Answered by mr W last updated on 20/Jan/22
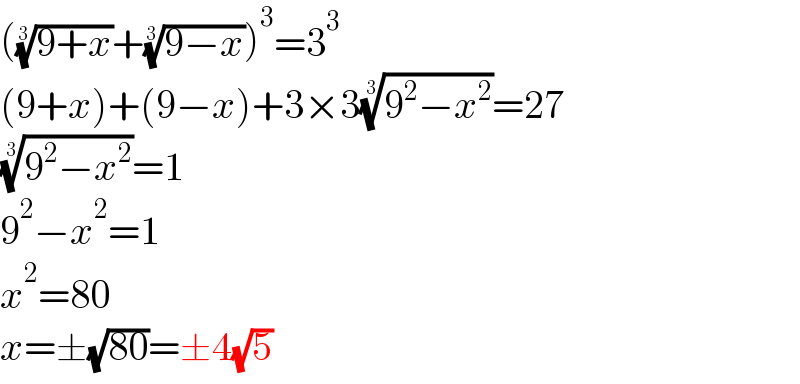
$$\left(\sqrt[{\mathrm{3}}]{\mathrm{9}+{x}}+\sqrt[{\mathrm{3}}]{\mathrm{9}−{x}}\right)^{\mathrm{3}} =\mathrm{3}^{\mathrm{3}} \\ $$$$\left(\mathrm{9}+{x}\right)+\left(\mathrm{9}−{x}\right)+\mathrm{3}×\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{9}^{\mathrm{2}} −{x}^{\mathrm{2}} }=\mathrm{27} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{9}^{\mathrm{2}} −{x}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\mathrm{9}^{\mathrm{2}} −{x}^{\mathrm{2}} =\mathrm{1} \\ $$$${x}^{\mathrm{2}} =\mathrm{80} \\ $$$${x}=\pm\sqrt{\mathrm{80}}=\pm\mathrm{4}\sqrt{\mathrm{5}} \\ $$
