Question Number 163163 by mathlove last updated on 04/Jan/22
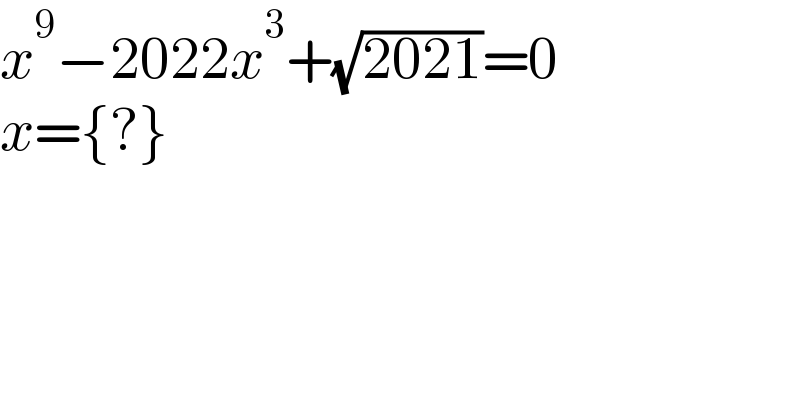
$${x}^{\mathrm{9}} −\mathrm{2022}{x}^{\mathrm{3}} +\sqrt{\mathrm{2021}}=\mathrm{0} \\ $$$${x}=\left\{?\right\} \\ $$
Commented by mr W last updated on 04/Jan/22
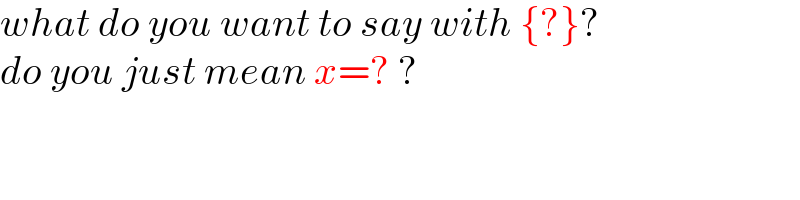
$${what}\:{do}\:{you}\:{want}\:{to}\:{say}\:{with}\:\left\{?\right\}? \\ $$$${do}\:{you}\:{just}\:{mean}\:{x}=?\:? \\ $$
Answered by mr W last updated on 04/Jan/22
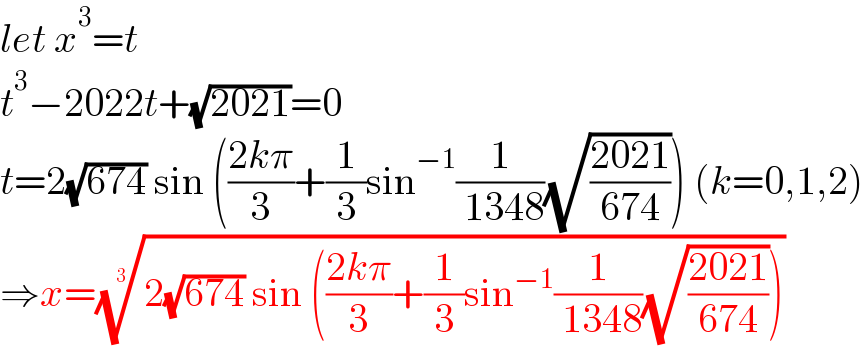
$${let}\:{x}^{\mathrm{3}} ={t} \\ $$$${t}^{\mathrm{3}} −\mathrm{2022}{t}+\sqrt{\mathrm{2021}}=\mathrm{0} \\ $$$${t}=\mathrm{2}\sqrt{\mathrm{674}}\:\mathrm{sin}\:\left(\frac{\mathrm{2}{k}\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\mathrm{1348}}\sqrt{\frac{\mathrm{2021}}{\mathrm{674}}}\right)\:\left({k}=\mathrm{0},\mathrm{1},\mathrm{2}\right) \\ $$$$\Rightarrow{x}=\sqrt[{\mathrm{3}}]{\mathrm{2}\sqrt{\mathrm{674}}\:\mathrm{sin}\:\left(\frac{\mathrm{2}{k}\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\mathrm{1348}}\sqrt{\frac{\mathrm{2021}}{\mathrm{674}}}\right)} \\ $$
