Question Number 83259 by 09658867628 last updated on 29/Feb/20
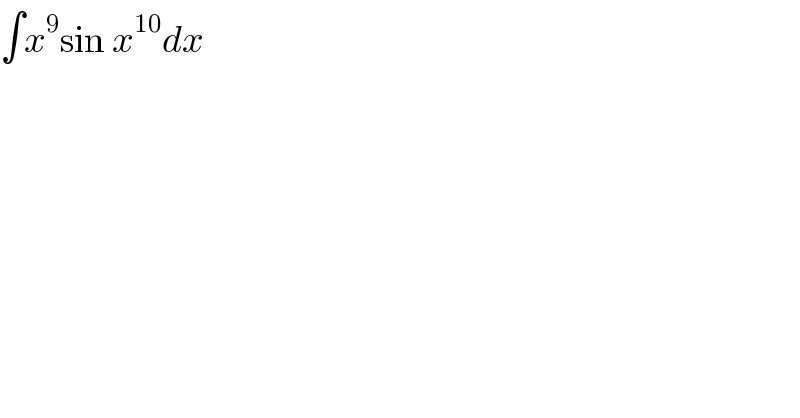
$$\int{x}^{\mathrm{9}} \mathrm{sin}\:{x}^{\mathrm{10}} {dx} \\ $$
Answered by TANMAY PANACEA last updated on 29/Feb/20
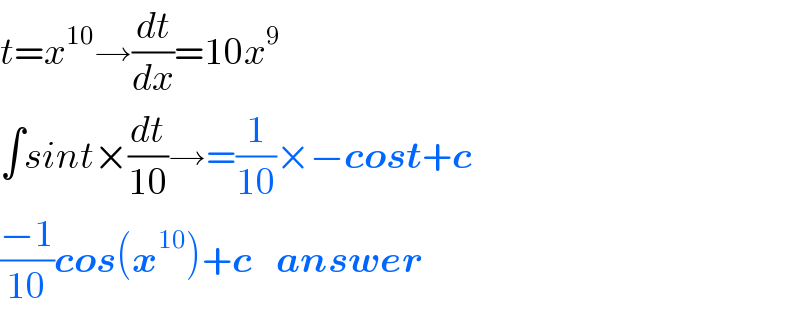
$${t}={x}^{\mathrm{10}} \rightarrow\frac{{dt}}{{dx}}=\mathrm{10}{x}^{\mathrm{9}} \\ $$$$\int{sint}×\frac{{dt}}{\mathrm{10}}\rightarrow=\frac{\mathrm{1}}{\mathrm{10}}×−\boldsymbol{{cost}}+\boldsymbol{{c}} \\ $$$$\frac{−\mathrm{1}}{\mathrm{10}}\boldsymbol{{cos}}\left(\boldsymbol{{x}}^{\mathrm{10}} \right)+\boldsymbol{{c}}\:\:\:\:\boldsymbol{{answer}} \\ $$
