Question Number 118270 by bramlexs22 last updated on 16/Oct/20
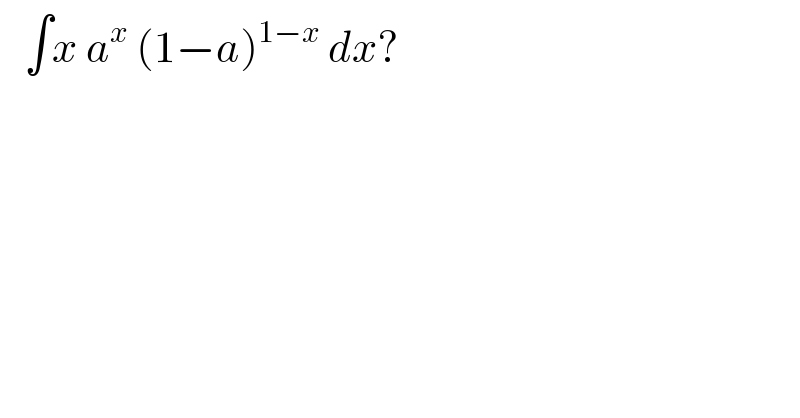
$$\:\:\:\int{x}\:{a}^{{x}} \:\left(\mathrm{1}−{a}\right)^{\mathrm{1}−{x}} \:{dx}? \\ $$
Commented by Dwaipayan Shikari last updated on 16/Oct/20
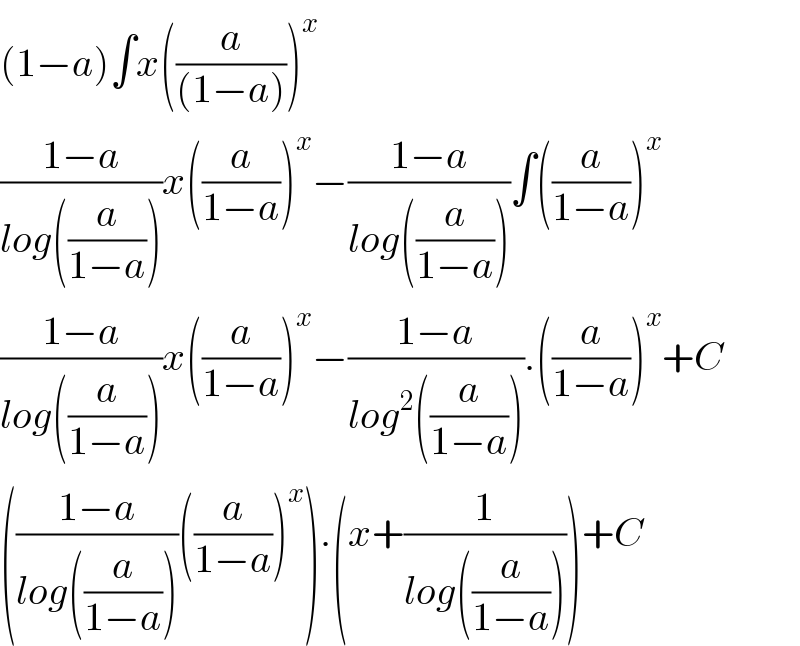
$$\left(\mathrm{1}−{a}\right)\int{x}\left(\frac{{a}}{\left(\mathrm{1}−{a}\right)}\right)^{{x}} \\ $$$$\frac{\mathrm{1}−{a}}{{log}\left(\frac{{a}}{\mathrm{1}−{a}}\right)}{x}\left(\frac{{a}}{\mathrm{1}−{a}}\right)^{{x}} −\frac{\mathrm{1}−{a}}{{log}\left(\frac{{a}}{\mathrm{1}−{a}}\right)}\int\left(\frac{{a}}{\mathrm{1}−{a}}\right)^{{x}} \\ $$$$\frac{\mathrm{1}−{a}}{{log}\left(\frac{{a}}{\mathrm{1}−{a}}\right)}{x}\left(\frac{{a}}{\mathrm{1}−{a}}\right)^{{x}} −\frac{\mathrm{1}−{a}}{{log}^{\mathrm{2}} \left(\frac{{a}}{\mathrm{1}−{a}}\right)}.\left(\frac{{a}}{\mathrm{1}−{a}}\right)^{{x}} +{C} \\ $$$$\left(\frac{\mathrm{1}−{a}}{{log}\left(\frac{{a}}{\mathrm{1}−{a}}\right)}\left(\frac{{a}}{\mathrm{1}−{a}}\right)^{{x}} \right).\left({x}+\frac{\mathrm{1}}{{log}\left(\frac{{a}}{\mathrm{1}−{a}}\right)}\right)+{C} \\ $$
