Question Number 80145 by behi83417@gmail.com last updated on 31/Jan/20
![{ (((x/a)+(y/b)=a^2 +b^2 )),(( [a,b∈R])),((ab(x^2 −y^2 )=xy(a^2 −b^2 ))) :}](https://www.tinkutara.com/question/Q80145.png)
$$\begin{cases}{\frac{\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{a}}}+\frac{\boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{b}}}=\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} }\\{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}}\in\boldsymbol{\mathrm{R}}\right]}\\{\boldsymbol{\mathrm{ab}}\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\boldsymbol{\mathrm{y}}^{\mathrm{2}} \right)=\boldsymbol{\mathrm{xy}}\left(\boldsymbol{\mathrm{a}}^{\mathrm{2}} −\boldsymbol{\mathrm{b}}^{\mathrm{2}} \right)}\end{cases} \\ $$
Commented by john santu last updated on 31/Jan/20
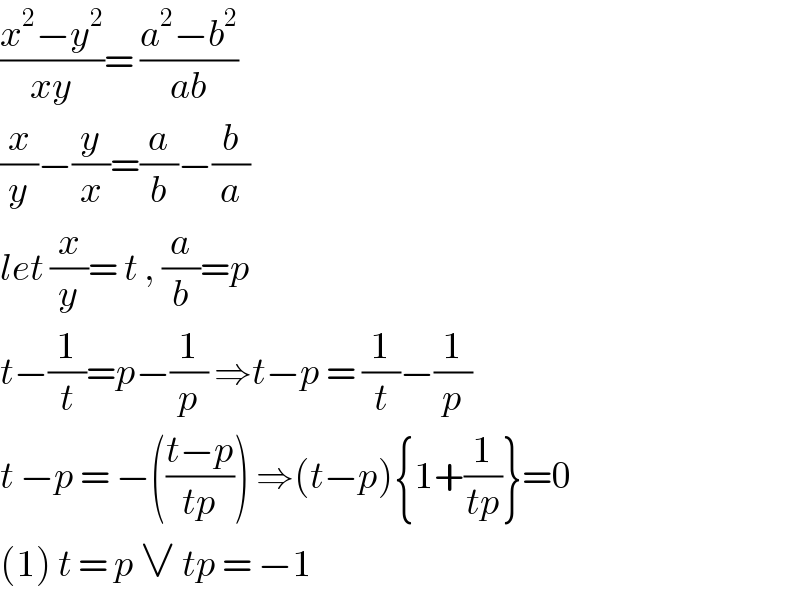
$$\frac{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }{{xy}}=\:\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{ab}} \\ $$$$\frac{{x}}{{y}}−\frac{{y}}{{x}}=\frac{{a}}{{b}}−\frac{{b}}{{a}} \\ $$$${let}\:\frac{{x}}{{y}}=\:{t}\:,\:\frac{{a}}{{b}}={p} \\ $$$${t}−\frac{\mathrm{1}}{{t}}={p}−\frac{\mathrm{1}}{{p}}\:\Rightarrow{t}−{p}\:=\:\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}}{{p}} \\ $$$${t}\:−{p}\:=\:−\left(\frac{{t}−{p}}{{tp}}\right)\:\Rightarrow\left({t}−{p}\right)\left\{\mathrm{1}+\frac{\mathrm{1}}{{tp}}\right\}=\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:{t}\:=\:{p}\:\vee\:{tp}\:=\:−\mathrm{1} \\ $$
Commented by john santu last updated on 31/Jan/20
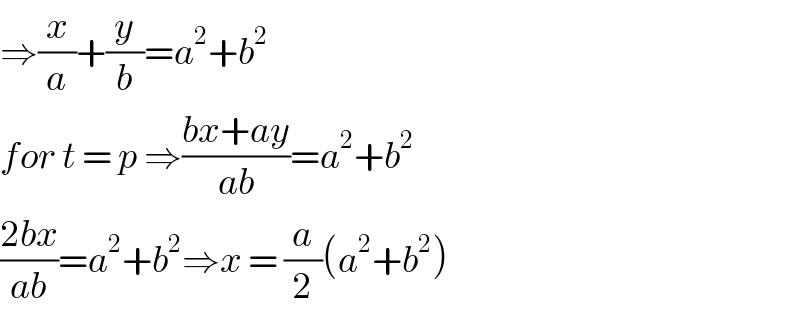
$$\Rightarrow\frac{{x}}{{a}}+\frac{{y}}{{b}}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$${for}\:{t}\:=\:{p}\:\Rightarrow\frac{{bx}+{ay}}{{ab}}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$\frac{\mathrm{2}{bx}}{{ab}}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \Rightarrow{x}\:=\:\frac{{a}}{\mathrm{2}}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$
Commented by john santu last updated on 31/Jan/20
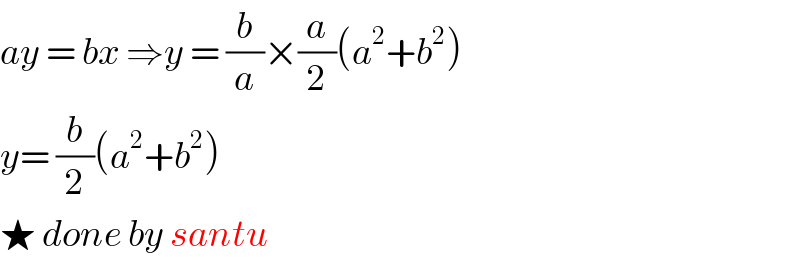
$${ay}\:=\:{bx}\:\Rightarrow{y}\:=\:\frac{{b}}{{a}}×\frac{{a}}{\mathrm{2}}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$$${y}=\:\frac{{b}}{\mathrm{2}}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\: \\ $$$$\bigstar\:{done}\:{by}\:{santu} \\ $$
Commented by jagoll last updated on 31/Jan/20

$${great}….{mister} \\ $$
Commented by behi83417@gmail.com last updated on 31/Jan/20

$$\mathrm{thanks}\:\mathrm{in}\:\mathrm{advance}\:\mathrm{sir}:\mathrm{santu}. \\ $$
Answered by MJS last updated on 31/Jan/20
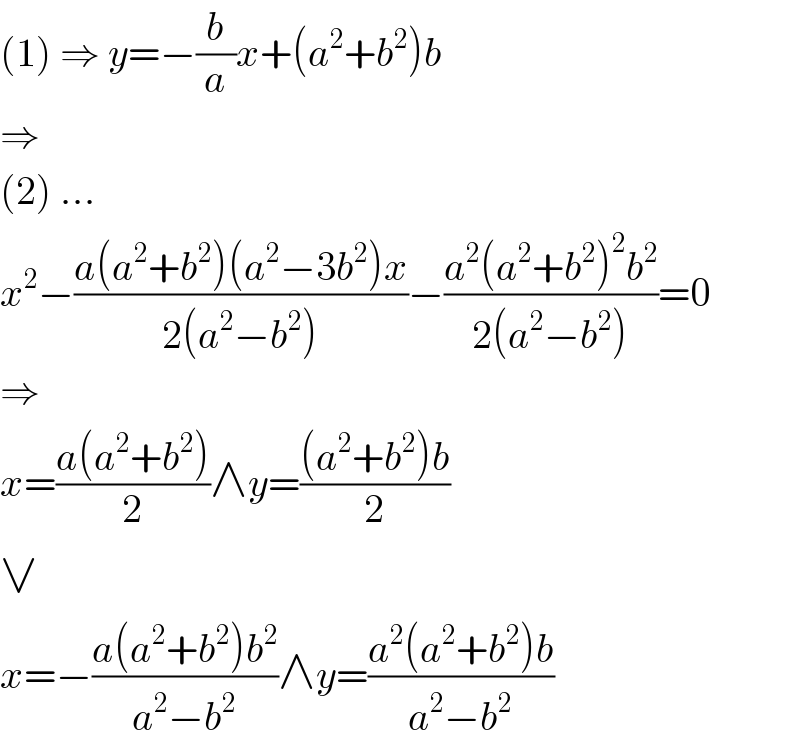
$$\left(\mathrm{1}\right)\:\Rightarrow\:{y}=−\frac{{b}}{{a}}{x}+\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){b} \\ $$$$\Rightarrow \\ $$$$\left(\mathrm{2}\right)\:… \\ $$$${x}^{\mathrm{2}} −\frac{{a}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left({a}^{\mathrm{2}} −\mathrm{3}{b}^{\mathrm{2}} \right){x}}{\mathrm{2}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}−\frac{{a}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} {b}^{\mathrm{2}} }{\mathrm{2}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${x}=\frac{{a}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}{\mathrm{2}}\wedge{y}=\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){b}}{\mathrm{2}} \\ $$$$\vee \\ $$$${x}=−\frac{{a}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){b}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\wedge{y}=\frac{{a}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){b}}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$
Commented by behi83417@gmail.com last updated on 31/Jan/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{proph}−:\mathrm{MJS} \\ $$
