Question Number 56264 by ajfour last updated on 13/Mar/19
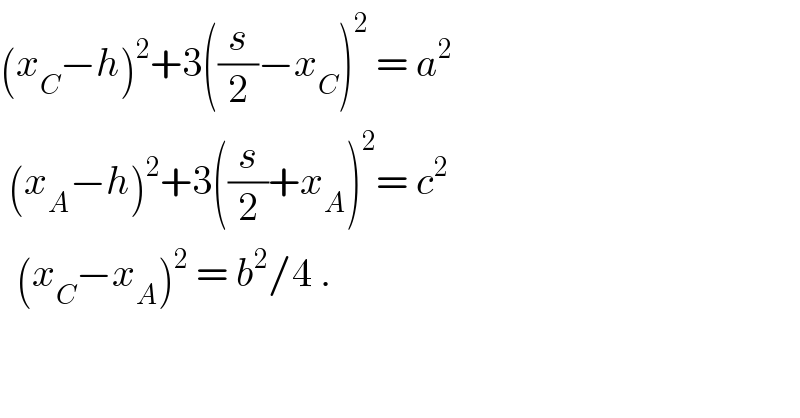
$$\left({x}_{{C}} −{h}\right)^{\mathrm{2}} +\mathrm{3}\left(\frac{{s}}{\mathrm{2}}−{x}_{{C}} \right)^{\mathrm{2}} \:=\:{a}^{\mathrm{2}} \\ $$$$\:\left({x}_{{A}} −{h}\right)^{\mathrm{2}} +\mathrm{3}\left(\frac{{s}}{\mathrm{2}}+{x}_{{A}} \right)^{\mathrm{2}} =\:{c}^{\mathrm{2}} \\ $$$$\:\:\left({x}_{{C}} −{x}_{{A}} \right)^{\mathrm{2}} \:=\:{b}^{\mathrm{2}} /\mathrm{4}\:. \\ $$
Commented by MJS last updated on 12/Mar/19

$$\mathrm{seems}\:\mathrm{impossible} \\ $$
Commented by ajfour last updated on 13/Mar/19
Commented by ajfour last updated on 13/Mar/19
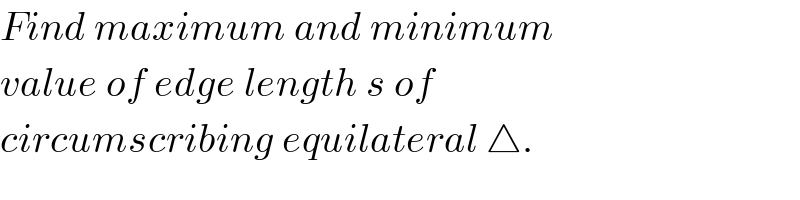
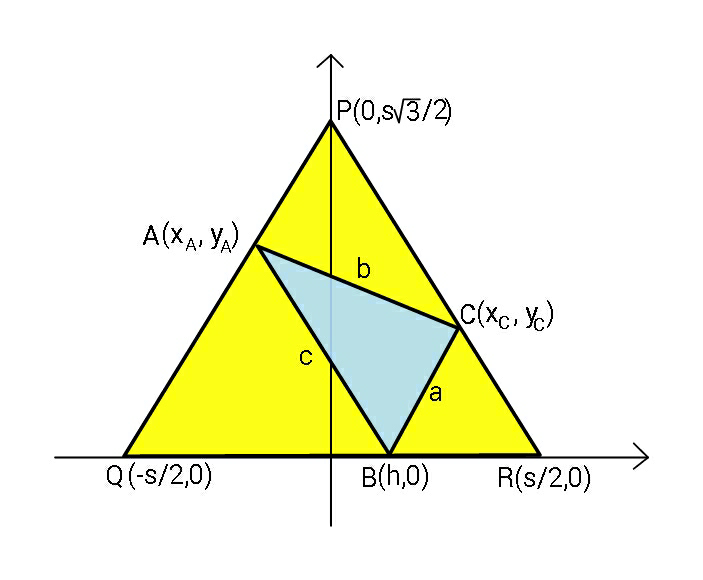
$${Find}\:{maximum}\:{and}\:{minimum} \\ $$$${value}\:{of}\:{edge}\:{length}\:{s}\:{of} \\ $$$${circumscribing}\:{equilateral}\:\bigtriangleup. \\ $$
