Question Number 113907 by bemath last updated on 16/Sep/20
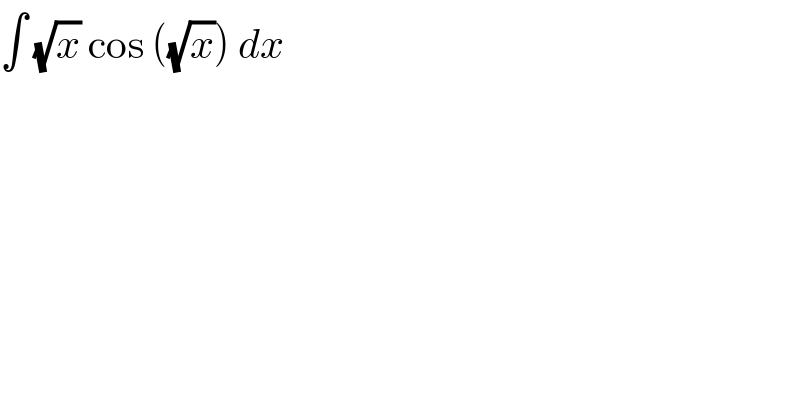
$$\int\:\sqrt{{x}}\:\mathrm{cos}\:\left(\sqrt{{x}}\right)\:{dx} \\ $$
Answered by bobhans last updated on 16/Sep/20
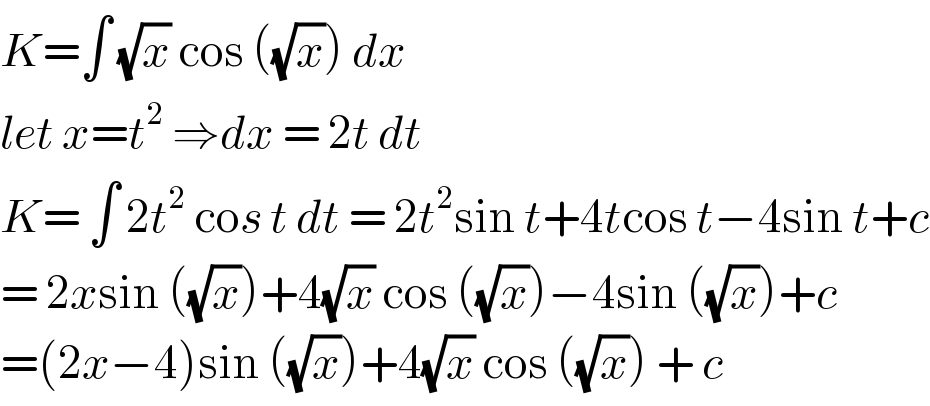
$${K}=\int\:\sqrt{{x}}\:\mathrm{cos}\:\left(\sqrt{{x}}\right)\:{dx}\: \\ $$$${let}\:{x}={t}^{\mathrm{2}} \:\Rightarrow{dx}\:=\:\mathrm{2}{t}\:{dt}\: \\ $$$${K}=\:\int\:\mathrm{2}{t}^{\mathrm{2}} \:\mathrm{co}{s}\:{t}\:{dt}\:=\:\mathrm{2}{t}^{\mathrm{2}} \mathrm{sin}\:{t}+\mathrm{4}{t}\mathrm{cos}\:{t}−\mathrm{4sin}\:{t}+{c} \\ $$$$=\:\mathrm{2}{x}\mathrm{sin}\:\left(\sqrt{{x}}\right)+\mathrm{4}\sqrt{{x}}\:\mathrm{cos}\:\left(\sqrt{{x}}\right)−\mathrm{4sin}\:\left(\sqrt{{x}}\right)+{c} \\ $$$$=\left(\mathrm{2}{x}−\mathrm{4}\right)\mathrm{sin}\:\left(\sqrt{{x}}\right)+\mathrm{4}\sqrt{{x}}\:\mathrm{cos}\:\left(\sqrt{{x}}\right)\:+\:{c} \\ $$
