Question Number 161181 by cortano last updated on 13/Dec/21
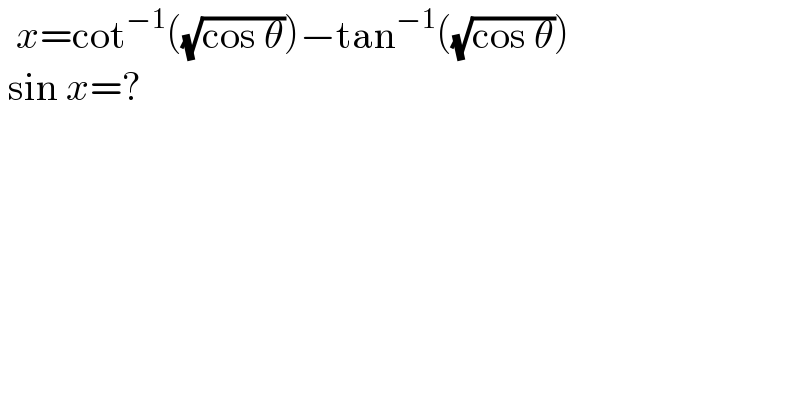
$$\:\:{x}=\mathrm{cot}^{−\mathrm{1}} \left(\sqrt{\mathrm{cos}\:\theta}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{cos}\:\theta}\right) \\ $$$$\:\mathrm{sin}\:{x}=? \\ $$
Commented by MJS_new last updated on 13/Dec/21

$$\mathrm{sin}\:\left(\mathrm{arctan}\:{a}\:−\mathrm{arctan}\:{b}\right)\:=\frac{{a}−{b}}{\:\sqrt{\left({a}^{\mathrm{2}} +\mathrm{1}\right)\left({b}^{\mathrm{2}} +\mathrm{1}\right)}} \\ $$$$\mathrm{arccot}\:\left({r}\right)\:=\frac{\mathrm{1}}{\mathrm{arctan}\:{r}}\:\Rightarrow\:{a}=\frac{\mathrm{1}}{{b}} \\ $$$$\Rightarrow \\ $$$$\frac{{a}−{b}}{\:\sqrt{\left({a}^{\mathrm{2}} +\mathrm{1}\right)\left({b}^{\mathrm{2}} +\mathrm{1}\right)}}=\frac{\mathrm{1}−{b}^{\mathrm{2}} }{\mathrm{1}+{b}^{\mathrm{2}} } \\ $$$$\Rightarrow \\ $$$$\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{1}−\mathrm{cos}\:\theta}{\mathrm{1}+\mathrm{cos}\:\theta} \\ $$
