Question Number 25290 by rather ishfaq last updated on 07/Dec/17

$$\int\frac{{x}\:{dx}}{\:\sqrt{{a}^{\mathrm{4}} +{x}^{\mathrm{4}} }} \\ $$
Answered by prakash jain last updated on 07/Dec/17
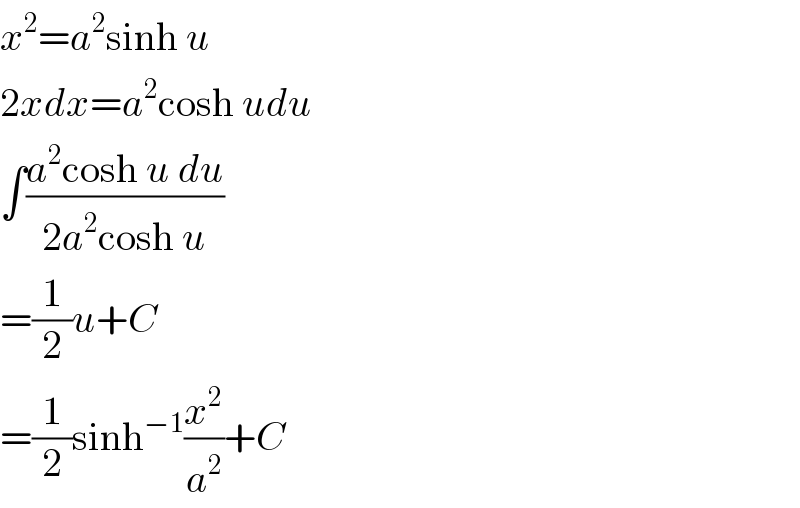
$${x}^{\mathrm{2}} ={a}^{\mathrm{2}} \mathrm{sinh}\:{u} \\ $$$$\mathrm{2}{xdx}={a}^{\mathrm{2}} \mathrm{cosh}\:{udu} \\ $$$$\int\frac{{a}^{\mathrm{2}} \mathrm{cosh}\:{u}\:{du}}{\mathrm{2}{a}^{\mathrm{2}} \mathrm{cosh}\:{u}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{u}+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinh}^{−\mathrm{1}} \frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+{C} \\ $$
Answered by ajfour last updated on 07/Dec/17
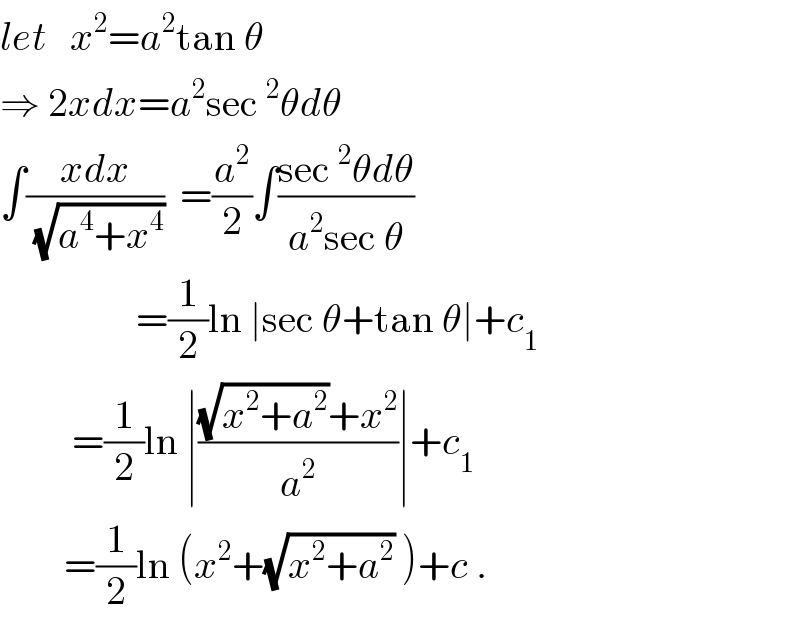
$${let}\:\:\:{x}^{\mathrm{2}} ={a}^{\mathrm{2}} \mathrm{tan}\:\theta \\ $$$$\Rightarrow\:\mathrm{2}{xdx}={a}^{\mathrm{2}} \mathrm{sec}\:^{\mathrm{2}} \theta{d}\theta \\ $$$$\int\frac{{xdx}}{\:\sqrt{{a}^{\mathrm{4}} +{x}^{\mathrm{4}} }}\:\:=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\int\frac{\mathrm{sec}\:^{\mathrm{2}} \theta{d}\theta}{{a}^{\mathrm{2}} \mathrm{sec}\:\theta} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{sec}\:\theta+\mathrm{tan}\:\theta\mid+{c}_{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\frac{\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }+{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\mid+{c}_{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({x}^{\mathrm{2}} +\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }\:\right)+{c}\:. \\ $$
