Question Number 81100 by jagoll last updated on 09/Feb/20
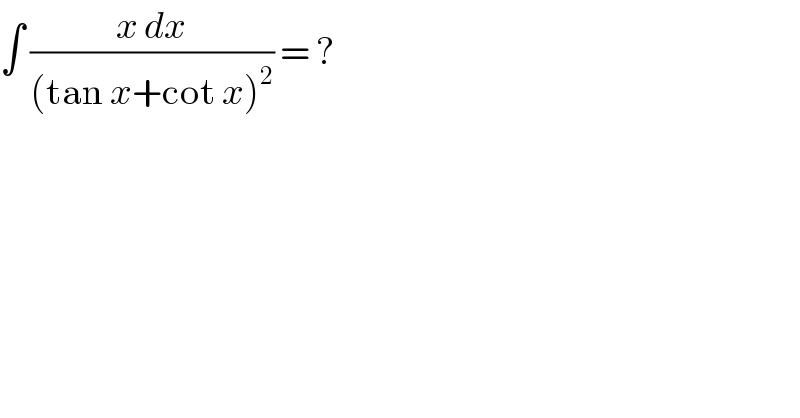
$$\int\:\frac{{x}\:{dx}}{\left(\mathrm{tan}\:{x}+\mathrm{cot}\:{x}\right)^{\mathrm{2}} }\:=\:? \\ $$
Commented by mind is power last updated on 09/Feb/20
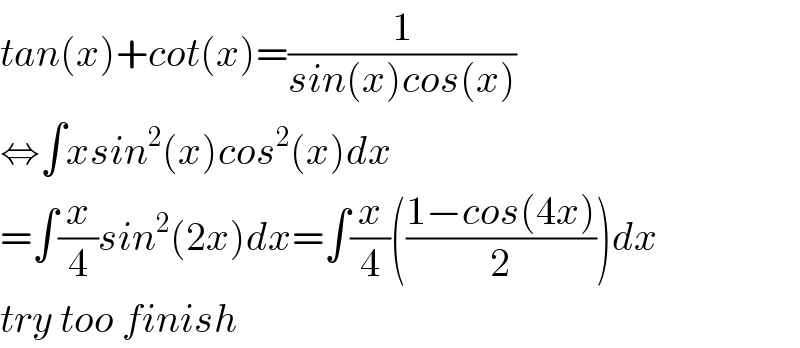
$${tan}\left({x}\right)+{cot}\left({x}\right)=\frac{\mathrm{1}}{{sin}\left({x}\right){cos}\left({x}\right)} \\ $$$$\Leftrightarrow\int{xsin}^{\mathrm{2}} \left({x}\right){cos}^{\mathrm{2}} \left({x}\right){dx} \\ $$$$=\int\frac{{x}}{\mathrm{4}}{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right){dx}=\int\frac{{x}}{\mathrm{4}}\left(\frac{\mathrm{1}−{cos}\left(\mathrm{4}{x}\right)}{\mathrm{2}}\right){dx} \\ $$$${try}\:{too}\:{finish} \\ $$
Commented by jagoll last updated on 09/Feb/20
$${thank}\:{you}\:{mister} \\ $$
