Question Number 150095 by mathdanisur last updated on 09/Aug/21
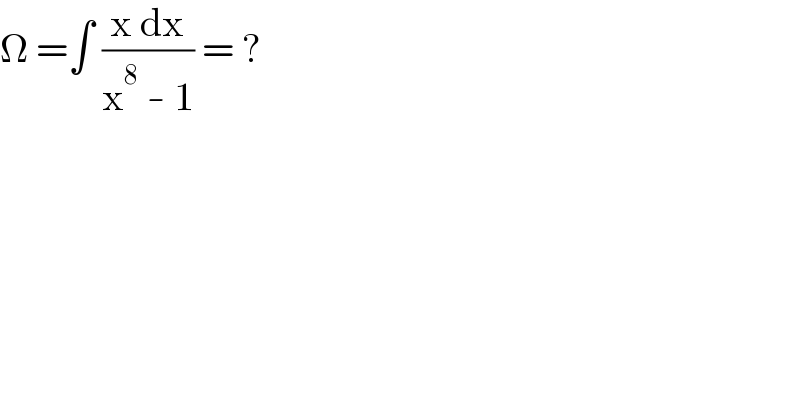
$$\Omega\:=\int\:\frac{\mathrm{x}\:\mathrm{dx}}{\mathrm{x}^{\mathrm{8}} \:-\:\mathrm{1}}\:=\:? \\ $$
Answered by Ar Brandon last updated on 09/Aug/21
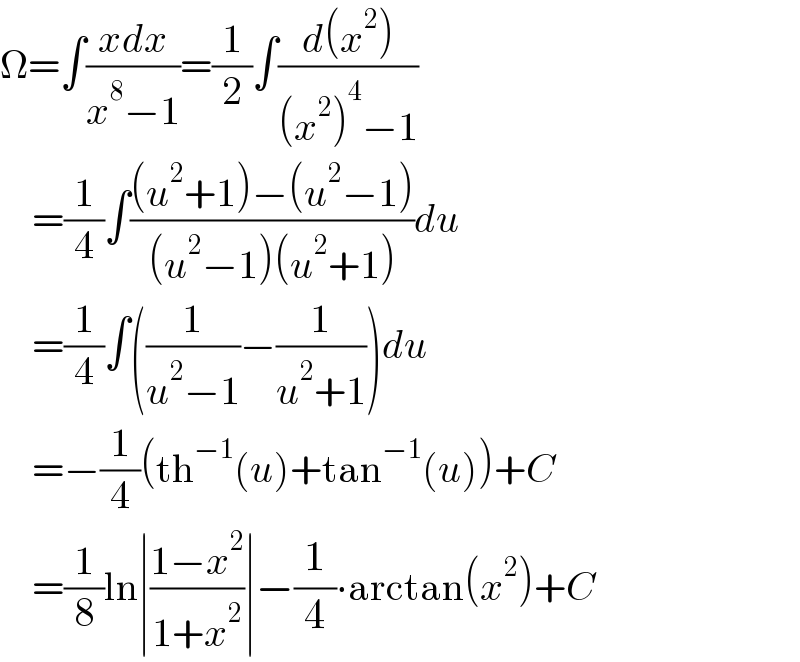
$$\Omega=\int\frac{{xdx}}{{x}^{\mathrm{8}} −\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} \right)^{\mathrm{4}} −\mathrm{1}} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\left({u}^{\mathrm{2}} +\mathrm{1}\right)−\left({u}^{\mathrm{2}} −\mathrm{1}\right)}{\left({u}^{\mathrm{2}} −\mathrm{1}\right)\left({u}^{\mathrm{2}} +\mathrm{1}\right)}{du} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int\left(\frac{\mathrm{1}}{{u}^{\mathrm{2}} −\mathrm{1}}−\frac{\mathrm{1}}{{u}^{\mathrm{2}} +\mathrm{1}}\right){du} \\ $$$$\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{th}^{−\mathrm{1}} \left({u}\right)+\mathrm{tan}^{−\mathrm{1}} \left({u}\right)\right)+{C} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{8}}\mathrm{ln}\mid\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\mid−\frac{\mathrm{1}}{\mathrm{4}}\centerdot\mathrm{arctan}\left({x}^{\mathrm{2}} \right)+{C} \\ $$
Commented by mathdanisur last updated on 09/Aug/21
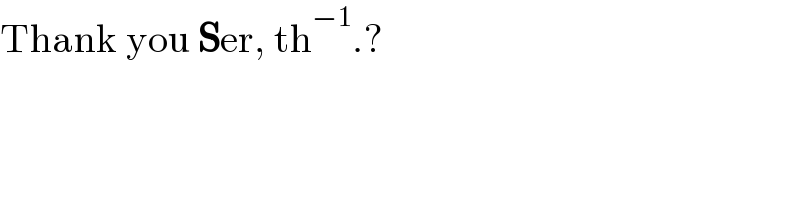
$$\mathrm{Thank}\:\mathrm{you}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{th}^{−\mathrm{1}} .? \\ $$
Commented by Ar Brandon last updated on 09/Aug/21

$$\mathrm{argtanh} \\ $$
Commented by mathdanisur last updated on 09/Aug/21

$$\mathrm{Thankyou}\:\mathrm{Ser} \\ $$
Commented by mathdanisur last updated on 09/Aug/21
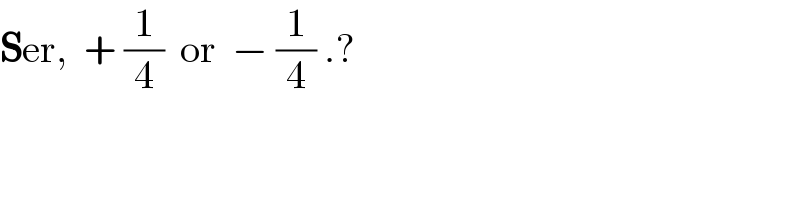
$$\boldsymbol{\mathrm{S}}\mathrm{er},\:\:+\:\frac{\mathrm{1}}{\mathrm{4}}\:\:\mathrm{or}\:\:−\:\frac{\mathrm{1}}{\mathrm{4}}\:.? \\ $$
Commented by Ar Brandon last updated on 09/Aug/21

$$−\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{thanks} \\ $$
Commented by mathdanisur last updated on 09/Aug/21

$$\mathrm{Thanks}\:\mathrm{Ser} \\ $$
Commented by Canebulok last updated on 09/Aug/21
How did you do that to make dx into d(x²) ?
Commented by Ar Brandon last updated on 09/Aug/21
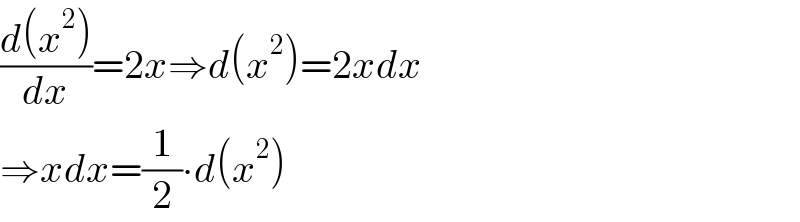
$$\frac{{d}\left({x}^{\mathrm{2}} \right)}{{dx}}=\mathrm{2}{x}\Rightarrow{d}\left({x}^{\mathrm{2}} \right)=\mathrm{2}{xdx} \\ $$$$\Rightarrow{xdx}=\frac{\mathrm{1}}{\mathrm{2}}\centerdot{d}\left({x}^{\mathrm{2}} \right) \\ $$
