Question Number 125054 by micelle last updated on 08/Dec/20
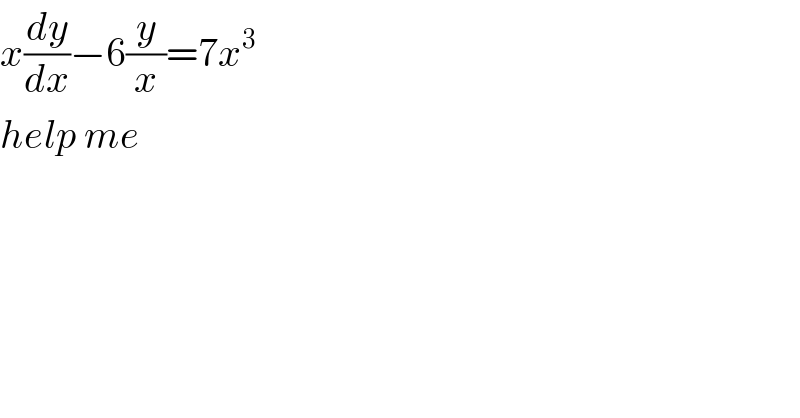
$${x}\frac{{dy}}{{dx}}−\mathrm{6}\frac{{y}}{{x}}=\mathrm{7}{x}^{\mathrm{3}} \\ $$$${help}\:{me} \\ $$
Answered by Dwaipayan Shikari last updated on 08/Dec/20
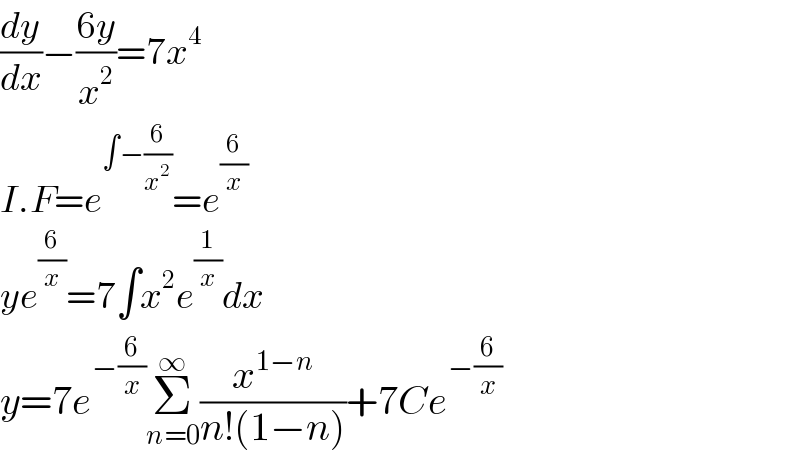
$$\frac{{dy}}{{dx}}−\frac{\mathrm{6}{y}}{{x}^{\mathrm{2}} }=\mathrm{7}{x}^{\mathrm{4}} \\ $$$${I}.{F}={e}^{\int−\frac{\mathrm{6}}{{x}^{\mathrm{2}} }} ={e}^{\frac{\mathrm{6}}{{x}}} \:\:\:\:\:\:\:\: \\ $$$${ye}^{\frac{\mathrm{6}}{{x}}} =\mathrm{7}\int{x}^{\mathrm{2}} {e}^{\frac{\mathrm{1}}{{x}}} {dx} \\ $$$${y}=\mathrm{7}{e}^{−\frac{\mathrm{6}}{{x}}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{1}−{n}} }{{n}!\left(\mathrm{1}−{n}\right)}+\mathrm{7}{Ce}^{−\frac{\mathrm{6}}{{x}}} \\ $$
Answered by TITA last updated on 08/Dec/20
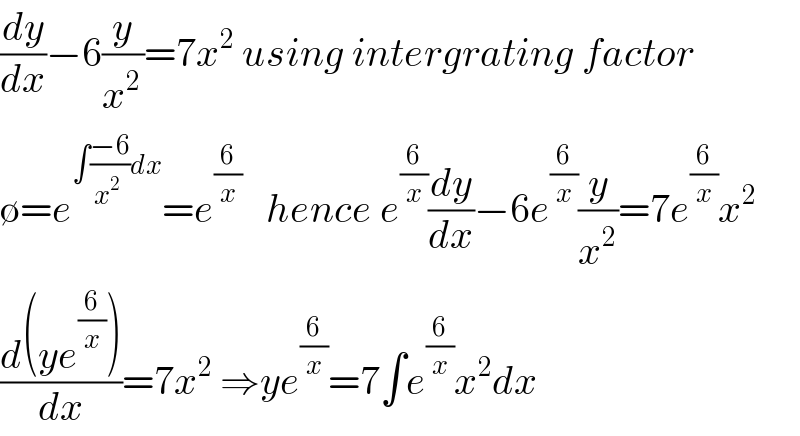
$$\frac{{dy}}{{dx}}−\mathrm{6}\frac{{y}}{{x}^{\mathrm{2}\:} }=\mathrm{7}{x}^{\mathrm{2}} \:{using}\:{intergrating}\:{factor} \\ $$$$\emptyset={e}^{\int\frac{−\mathrm{6}}{{x}^{\mathrm{2}\:\:} }{dx}} ={e}^{\frac{\mathrm{6}}{{x}}} \:\:\:{hence}\:{e}^{\frac{\mathrm{6}}{{x}}} \frac{{dy}}{{dx}}−\mathrm{6}{e}^{\frac{\mathrm{6}}{{x}}} \frac{{y}}{{x}^{\mathrm{2}} }=\mathrm{7}{e}^{\frac{\mathrm{6}}{{x}}} {x}^{\mathrm{2}} \\ $$$$\frac{{d}\left({ye}^{\frac{\mathrm{6}}{{x}}} \right)}{{dx}}=\mathrm{7}{x}^{\mathrm{2}} \:\Rightarrow{ye}^{\frac{\mathrm{6}}{{x}}} =\mathrm{7}\int{e}^{\frac{\mathrm{6}}{{x}}} {x}^{\mathrm{2}} {dx} \\ $$
Commented by TITA last updated on 08/Dec/20
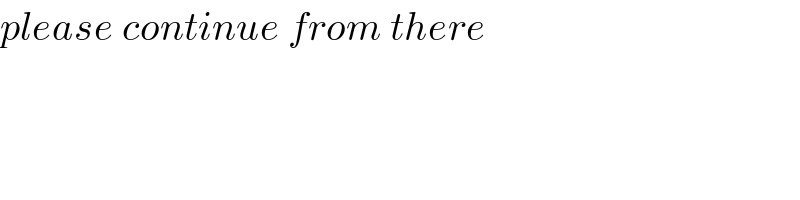
$${please}\:{continue}\:{from}\:{there} \\ $$
Commented by benjo_mathlover last updated on 08/Dec/20

$${it}\:{should}\:{be}\:{ye}^{\frac{\mathrm{6}}{{x}}} \:=\:\int\:\mathrm{7}{x}^{\mathrm{2}} {e}^{\frac{\mathrm{6}}{{x}}} \:{dx}. \\ $$$${your}\:{solution}\:{is}\:{wrong} \\ $$
Commented by TITA last updated on 08/Dec/20

$${ok}\:{thanks} \\ $$
Commented by mohammad17 last updated on 08/Dec/20

$${false}\:{solution} \\ $$
Answered by Bird last updated on 08/Dec/20
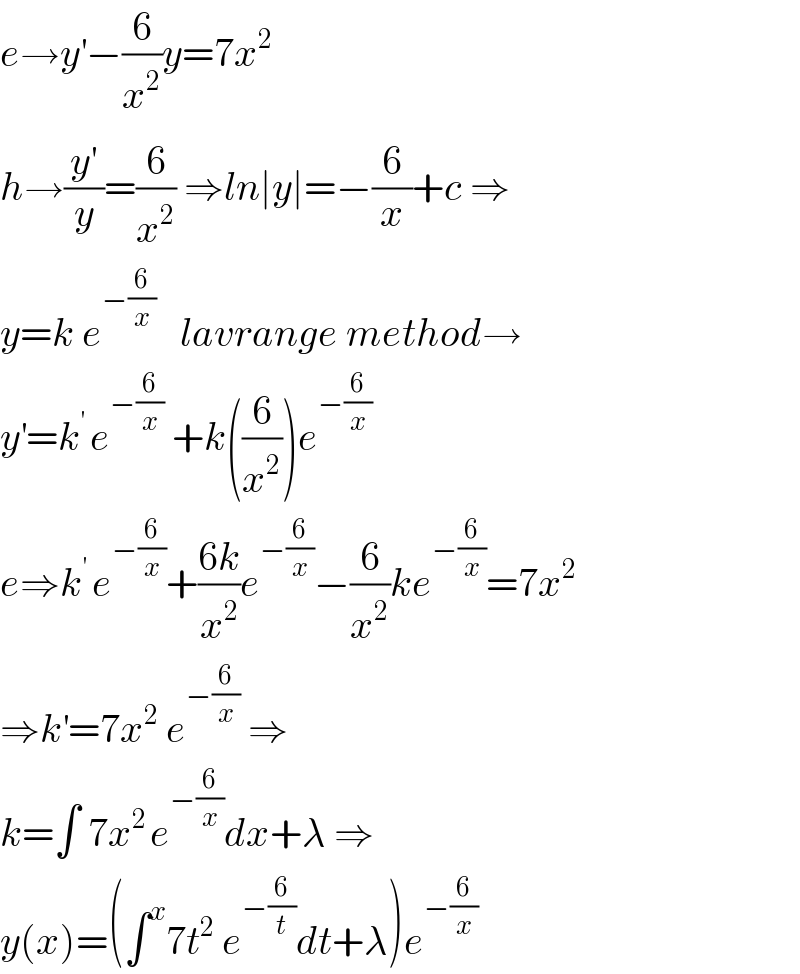
$${e}\rightarrow{y}^{'} −\frac{\mathrm{6}}{{x}^{\mathrm{2}} }{y}=\mathrm{7}{x}^{\mathrm{2}} \\ $$$${h}\rightarrow\frac{{y}^{'} }{{y}}=\frac{\mathrm{6}}{{x}^{\mathrm{2}} }\:\Rightarrow{ln}\mid{y}\mid=−\frac{\mathrm{6}}{{x}}+{c}\:\Rightarrow \\ $$$${y}={k}\:{e}^{−\frac{\mathrm{6}}{{x}}} \:\:\:{lavrange}\:{method}\rightarrow \\ $$$${y}^{'} ={k}^{'\:} {e}^{−\frac{\mathrm{6}}{{x}}} \:+{k}\left(\frac{\mathrm{6}}{{x}^{\mathrm{2}} }\right){e}^{−\frac{\mathrm{6}}{{x}}} \\ $$$${e}\Rightarrow{k}^{'\:} {e}^{−\frac{\mathrm{6}}{{x}}} +\frac{\mathrm{6}{k}}{{x}^{\mathrm{2}} }{e}^{−\frac{\mathrm{6}}{{x}}} −\frac{\mathrm{6}}{{x}^{\mathrm{2}} }{ke}^{−\frac{\mathrm{6}}{{x}}} =\mathrm{7}{x}^{\mathrm{2}} \\ $$$$\Rightarrow{k}^{'} =\mathrm{7}{x}^{\mathrm{2}} \:{e}^{−\frac{\mathrm{6}}{{x}}} \:\Rightarrow \\ $$$${k}=\int\:\mathrm{7}{x}^{\mathrm{2}\:} {e}^{−\frac{\mathrm{6}}{{x}}} {dx}+\lambda\:\Rightarrow \\ $$$${y}\left({x}\right)=\left(\int^{{x}} \mathrm{7}{t}^{\mathrm{2}} \:{e}^{−\frac{\mathrm{6}}{{t}}} {dt}+\lambda\right){e}^{−\frac{\mathrm{6}}{{x}}} \\ $$
