Question Number 118962 by benjo_mathlover last updated on 21/Oct/20
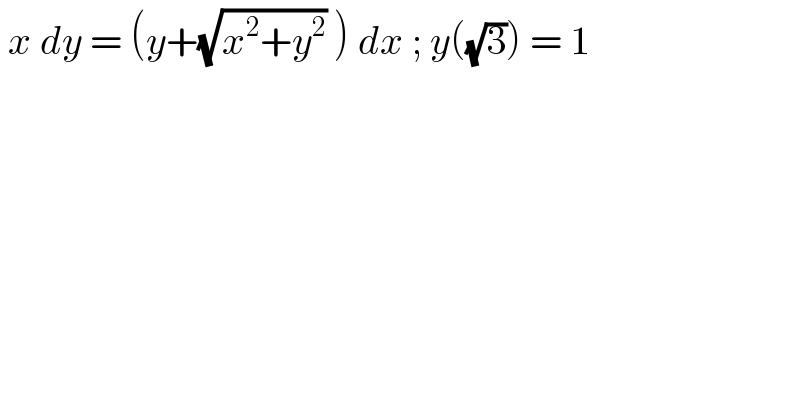
$$\:{x}\:{dy}\:=\:\left({y}+\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\right)\:{dx}\:;\:{y}\left(\sqrt{\mathrm{3}}\right)\:=\:\mathrm{1} \\ $$
Answered by TANMAY PANACEA last updated on 21/Oct/20
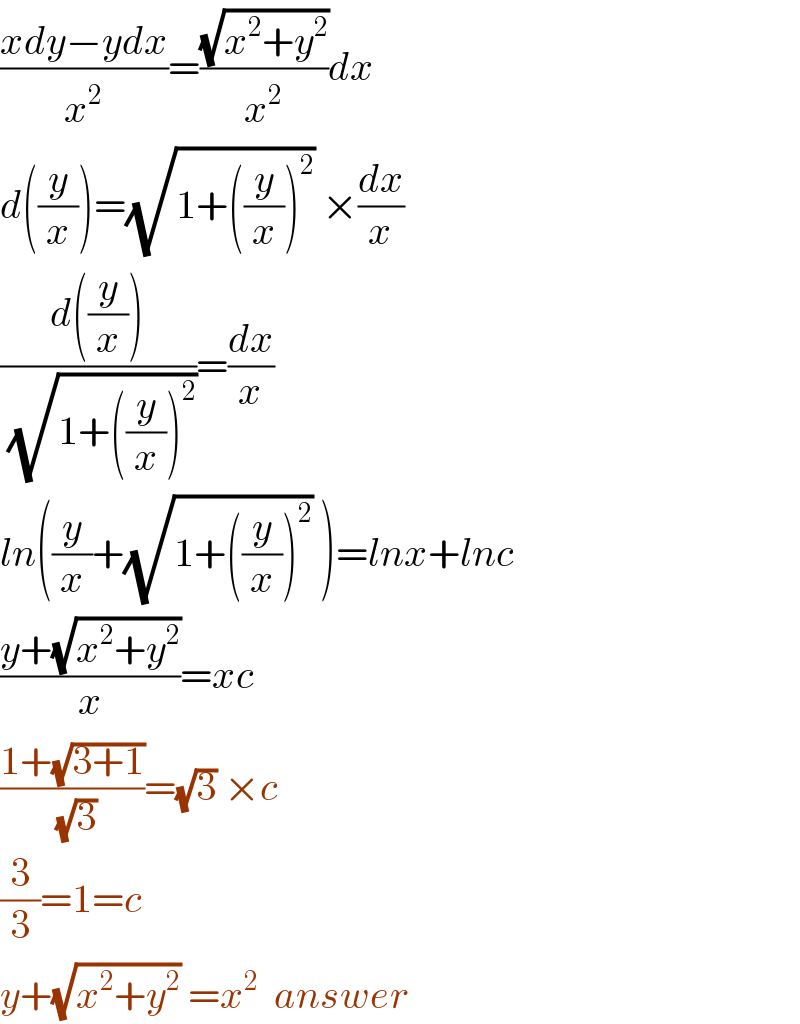
$$\frac{{xdy}−{ydx}}{{x}^{\mathrm{2}} }=\frac{\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}{{x}^{\mathrm{2}} }{dx} \\ $$$${d}\left(\frac{{y}}{{x}}\right)=\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }\:×\frac{{dx}}{{x}} \\ $$$$\frac{{d}\left(\frac{{y}}{{x}}\right)}{\:\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }}=\frac{{dx}}{{x}} \\ $$$${ln}\left(\frac{{y}}{{x}}+\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }\:\right)={lnx}+{lnc} \\ $$$$\frac{{y}+\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}{{x}}={xc} \\ $$$$\frac{\mathrm{1}+\sqrt{\mathrm{3}+\mathrm{1}}}{\:\sqrt{\mathrm{3}}}=\sqrt{\mathrm{3}}\:×{c} \\ $$$$\frac{\mathrm{3}}{\mathrm{3}}=\mathrm{1}={c} \\ $$$${y}+\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:={x}^{\mathrm{2}} \:\:{answer} \\ $$
Answered by bramlexs22 last updated on 21/Oct/20
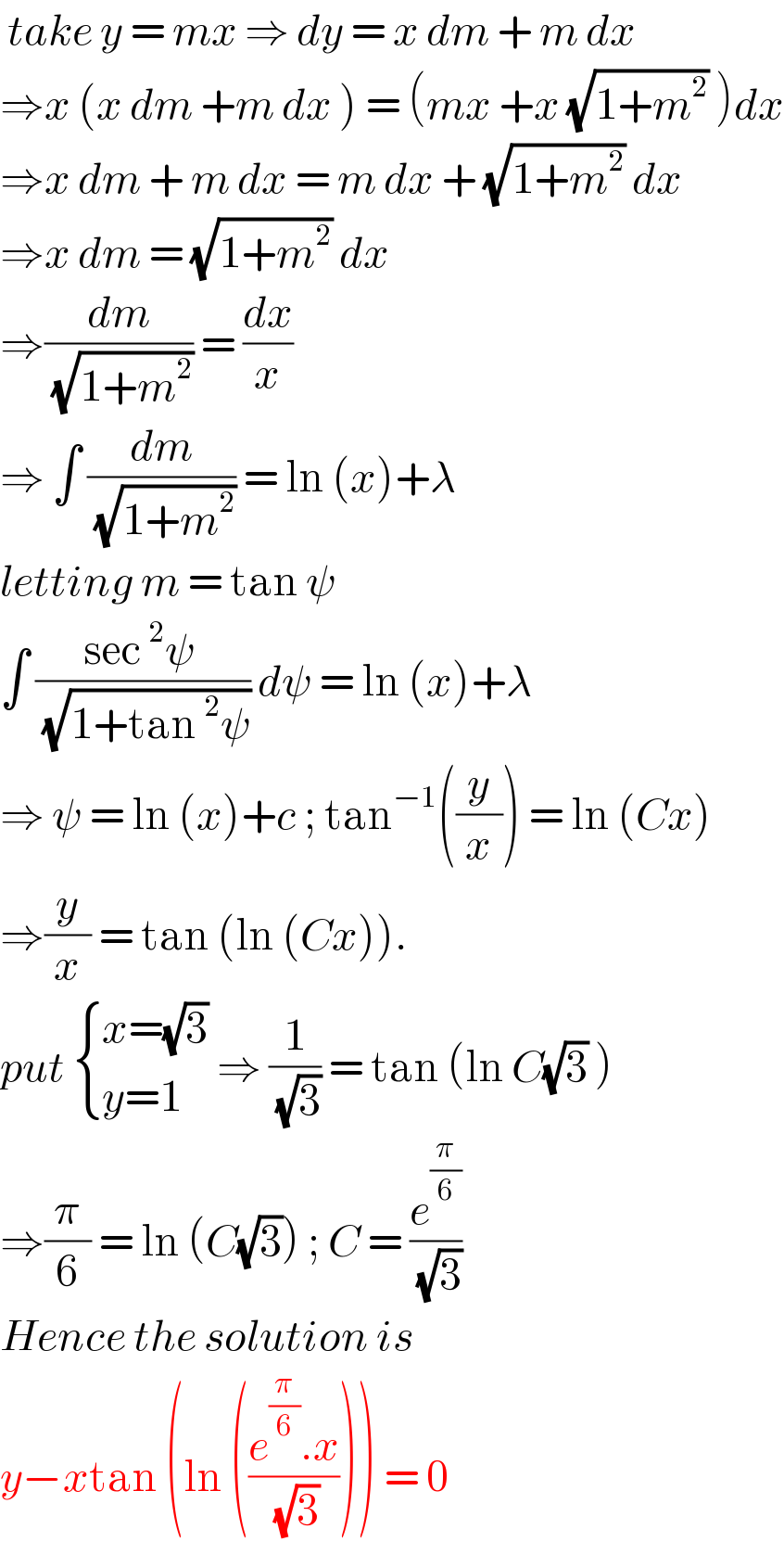
$$\:{take}\:{y}\:=\:{mx}\:\Rightarrow\:{dy}\:=\:{x}\:{dm}\:+\:{m}\:{dx}\: \\ $$$$\Rightarrow{x}\:\left({x}\:{dm}\:+{m}\:{dx}\:\right)\:=\:\left({mx}\:+{x}\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }\:\right){dx} \\ $$$$\Rightarrow{x}\:{dm}\:+\:{m}\:{dx}\:=\:{m}\:{dx}\:+\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }\:{dx} \\ $$$$\Rightarrow{x}\:{dm}\:=\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }\:{dx}\: \\ $$$$\Rightarrow\frac{{dm}}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}\:=\:\frac{{dx}}{{x}} \\ $$$$\Rightarrow\:\int\:\frac{{dm}}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}\:=\:\mathrm{ln}\:\left({x}\right)+\lambda\: \\ $$$${letting}\:{m}\:=\:\mathrm{tan}\:\psi\: \\ $$$$\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \psi\:}{\:\sqrt{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \psi}}\:{d}\psi\:=\:\mathrm{ln}\:\left({x}\right)+\lambda \\ $$$$\Rightarrow\:\psi\:=\:\mathrm{ln}\:\left({x}\right)+{c}\:;\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{{y}}{{x}}\right)\:=\:\mathrm{ln}\:\left({Cx}\right) \\ $$$$\Rightarrow\frac{{y}}{{x}}\:=\:\mathrm{tan}\:\left(\mathrm{ln}\:\left({Cx}\right)\right). \\ $$$${put}\:\begin{cases}{{x}=\sqrt{\mathrm{3}}}\\{{y}=\mathrm{1}}\end{cases}\:\Rightarrow\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:=\:\mathrm{tan}\:\left(\mathrm{ln}\:{C}\sqrt{\mathrm{3}}\:\right) \\ $$$$\Rightarrow\frac{\pi}{\mathrm{6}}\:=\:\mathrm{ln}\:\left({C}\sqrt{\mathrm{3}}\right)\:;\:{C}\:=\:\frac{{e}^{\frac{\pi}{\mathrm{6}}} }{\:\sqrt{\mathrm{3}}} \\ $$$${Hence}\:{the}\:{solution}\:{is}\: \\ $$$${y}−{x}\mathrm{tan}\:\left(\mathrm{ln}\:\left(\frac{{e}^{\frac{\pi}{\mathrm{6}}} .{x}}{\:\sqrt{\mathrm{3}}}\right)\right)\:=\:\mathrm{0} \\ $$
