Question Number 62453 by Tawa1 last updated on 21/Jun/19
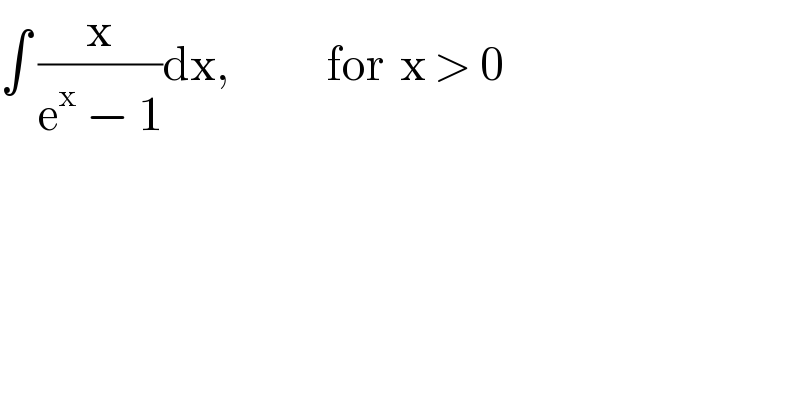
$$\int\:\frac{\mathrm{x}}{\mathrm{e}^{\mathrm{x}} \:−\:\mathrm{1}}\mathrm{dx},\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{for}\:\:\mathrm{x}\:>\:\mathrm{0} \\ $$
Commented by mathmax by abdo last updated on 21/Jun/19
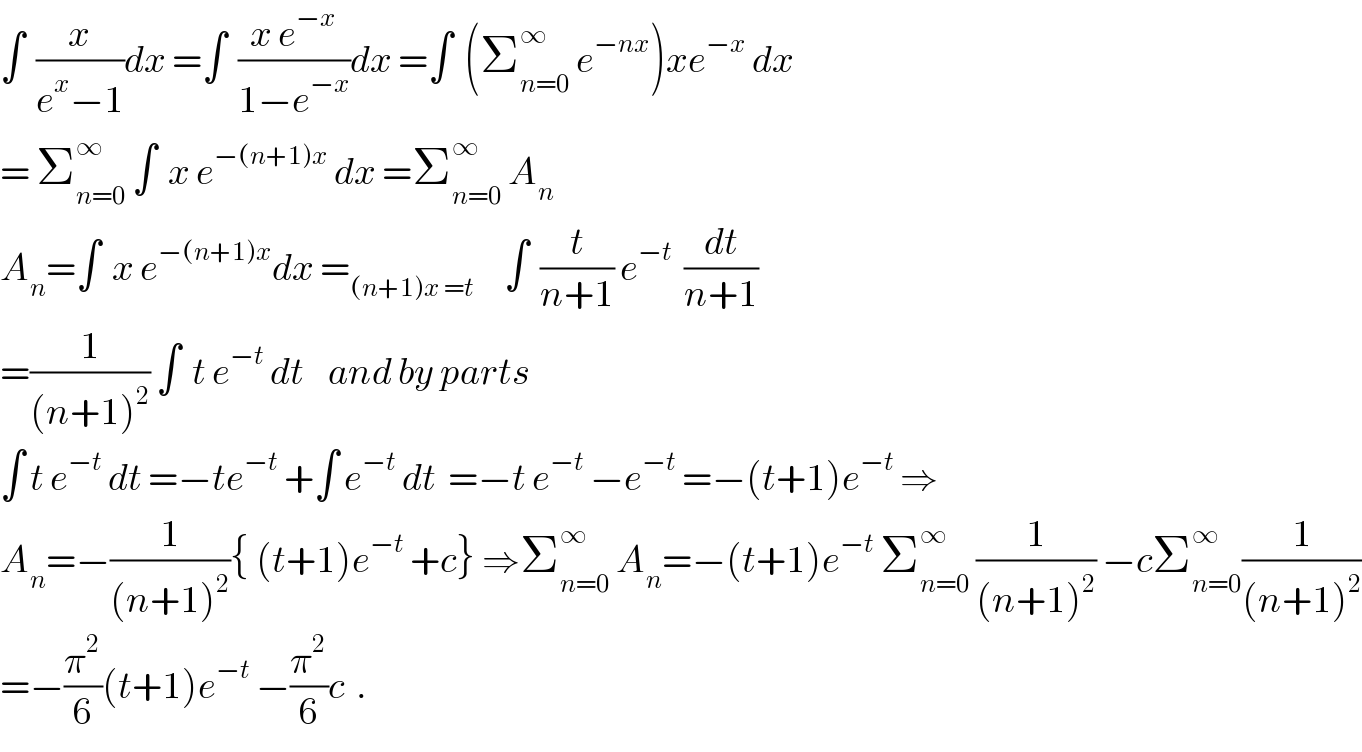
$$\int\:\:\frac{{x}}{{e}^{{x}} −\mathrm{1}}{dx}\:=\int\:\:\frac{{x}\:{e}^{−{x}} }{\mathrm{1}−{e}^{−{x}} }{dx}\:=\int\:\:\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:{e}^{−{nx}} \right){xe}^{−{x}} \:{dx} \\ $$$$=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\int\:\:{x}\:{e}^{−\left({n}+\mathrm{1}\right){x}} \:{dx}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:{A}_{{n}} \\ $$$${A}_{{n}} =\int\:\:{x}\:{e}^{−\left({n}+\mathrm{1}\right){x}} {dx}\:=_{\left({n}+\mathrm{1}\right){x}\:={t}} \:\:\:\:\:\int\:\:\frac{{t}}{{n}+\mathrm{1}}\:{e}^{−{t}} \:\:\frac{{dt}}{{n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:\int\:\:{t}\:{e}^{−{t}} \:{dt}\:\:\:\:{and}\:{by}\:{parts}\: \\ $$$$\int\:{t}\:{e}^{−{t}} \:{dt}\:=−{te}^{−{t}} \:+\int\:{e}^{−{t}} \:{dt}\:\:=−{t}\:{e}^{−{t}} \:−{e}^{−{t}} \:=−\left({t}+\mathrm{1}\right){e}^{−{t}} \:\Rightarrow \\ $$$${A}_{{n}} =−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\left\{\:\left({t}+\mathrm{1}\right){e}^{−{t}} \:+{c}\right\}\:\Rightarrow\sum_{{n}=\mathrm{0}} ^{\infty} \:{A}_{{n}} =−\left({t}+\mathrm{1}\right){e}^{−{t}} \:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:−{c}\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\left({t}+\mathrm{1}\right){e}^{−{t}} \:−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}{c}\:\:. \\ $$
Commented by Tawa1 last updated on 21/Jun/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mathmax by abdo last updated on 22/Jun/19
$${you}\:{are}\:{most}\:{welcome}. \\ $$
