Question Number 26244 by abdo imad last updated on 22/Dec/17
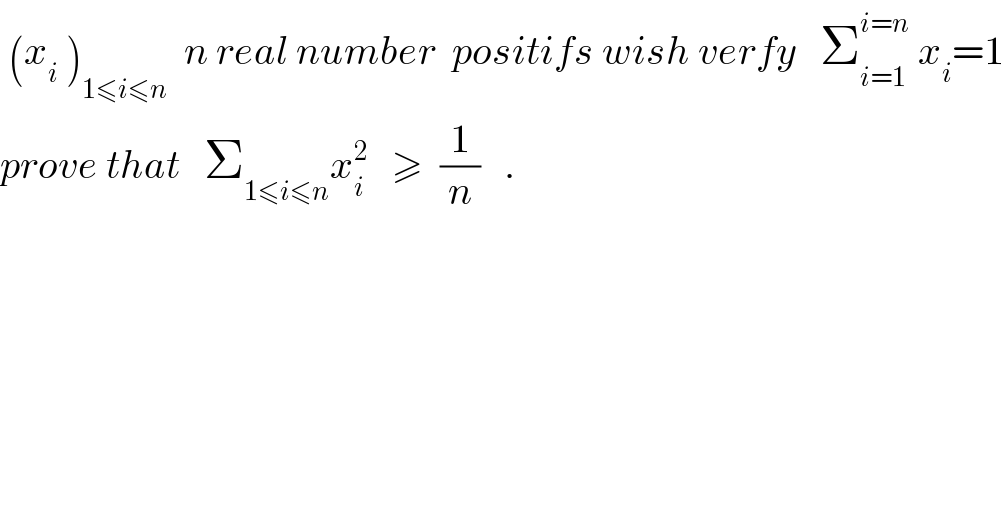
$$\:\left({x}_{{i}} \:\right)_{\mathrm{1}\leqslant{i}\leqslant{n}} \:\:{n}\:{real}\:{number}\:\:{positifs}\:{wish}\:{verfy}\:\:\:\sum_{{i}=\mathrm{1}} ^{{i}={n}} \:{x}_{{i}} =\mathrm{1} \\ $$$${prove}\:{that}\:\:\:\sum_{\mathrm{1}\leqslant{i}\leqslant{n}} {x}_{{i}} ^{\mathrm{2}} \:\:\:\geqslant\:\:\frac{\mathrm{1}}{{n}}\:\:\:. \\ $$
Commented by abdo imad last updated on 28/Dec/17
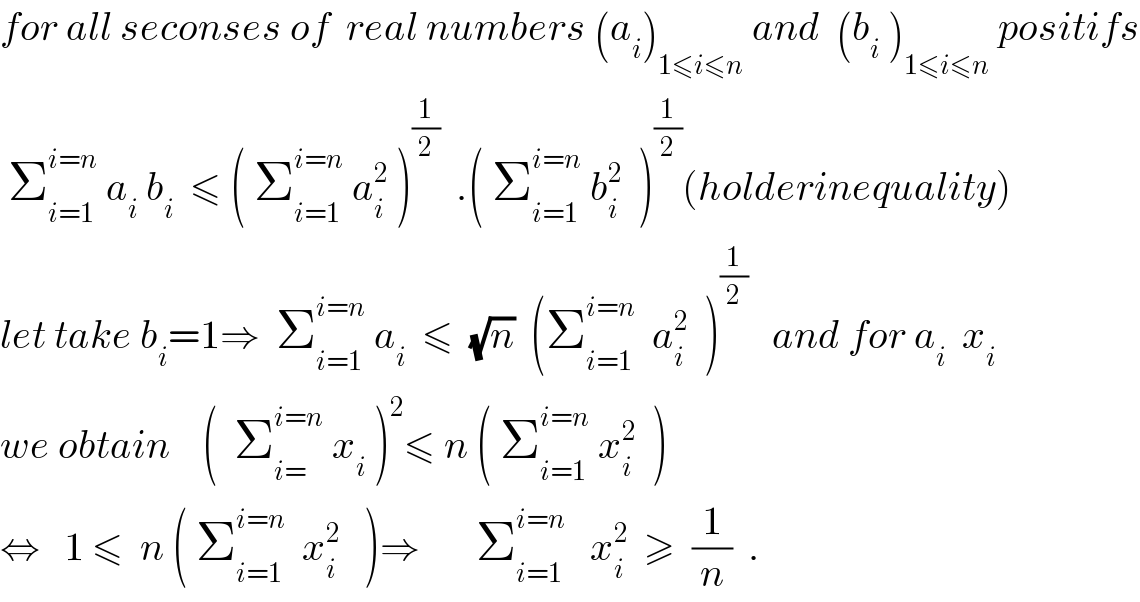
$${for}\:{all}\:{seconses}\:{of}\:\:{real}\:{numbers}\:\left({a}_{{i}} \right)_{\mathrm{1}\leqslant{i}\leqslant{n}} \:{and}\:\:\left({b}_{{i}} \:\right)_{\mathrm{1}\leqslant{i}\leqslant{n}} \:{positifs} \\ $$$$\:\sum_{{i}=\mathrm{1}} ^{{i}={n}} \:{a}_{{i}} \:{b}_{{i}} \:\:\leqslant\:\left(\:\sum_{{i}=\mathrm{1}} ^{{i}={n}} \:{a}_{{i}} ^{\mathrm{2}} \:\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:.\left(\:\sum_{{i}=\mathrm{1}} ^{{i}={n}} \:{b}_{{i}} ^{\mathrm{2}} \:\:\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \left({holderinequality}\right) \\ $$$${let}\:{take}\:{b}_{{i}} =\mathrm{1}\Rightarrow\:\:\sum_{{i}=\mathrm{1}} ^{{i}={n}} \:{a}_{{i}} \:\:\leqslant\:\:\sqrt{{n}}\:\:\left(\sum_{{i}=\mathrm{1}} ^{{i}={n}} \:\:{a}_{{i}} ^{\mathrm{2}} \:\:\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:\:{and}\:{for}\:{a}_{{i}} \:\:{x}_{{i}} \\ $$$${we}\:{obtain}\:\:\:\:\left(\:\:\sum_{{i}=} ^{{i}={n}} \:{x}_{{i}} \:\right)^{\mathrm{2}} \leqslant\:{n}\:\left(\:\sum_{{i}=\mathrm{1}} ^{{i}={n}} \:{x}_{{i}} ^{\mathrm{2}} \:\:\right) \\ $$$$\Leftrightarrow\:\:\:\mathrm{1}\:\leqslant\:\:{n}\:\left(\:\sum_{{i}=\mathrm{1}} ^{{i}={n}} \:\:{x}_{{i}} ^{\mathrm{2}} \:\:\:\right)\Rightarrow\:\:\:\:\:\:\:\sum_{{i}=\mathrm{1}} ^{{i}={n}} \:\:\:{x}_{{i}} ^{\mathrm{2}} \:\:\geqslant\:\:\frac{\mathrm{1}}{{n}}\:\:. \\ $$
