Question Number 60027 by aliesam last updated on 17/May/19

$$\int{x}^{{i}} {dx}=? \\ $$
Answered by MJS last updated on 17/May/19
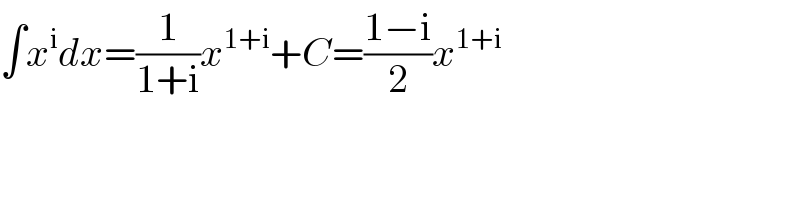
$$\int{x}^{\mathrm{i}} {dx}=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{i}}{x}^{\mathrm{1}+\mathrm{i}} +{C}=\frac{\mathrm{1}−\mathrm{i}}{\mathrm{2}}{x}^{\mathrm{1}+\mathrm{i}} \\ $$
Commented by MJS last updated on 17/May/19
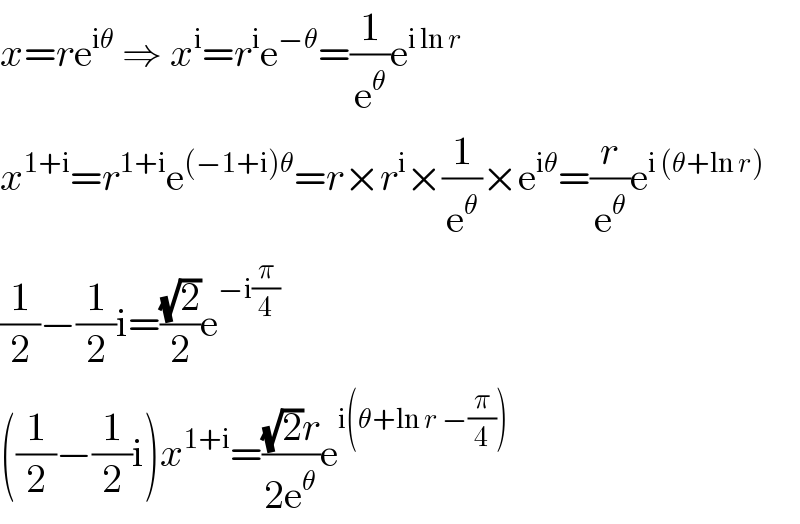
$${x}={r}\mathrm{e}^{\mathrm{i}\theta} \:\Rightarrow\:{x}^{\mathrm{i}} ={r}^{\mathrm{i}} \mathrm{e}^{−\theta} =\frac{\mathrm{1}}{\mathrm{e}^{\theta} }\mathrm{e}^{\mathrm{i}\:\mathrm{ln}\:{r}} \\ $$$${x}^{\mathrm{1}+\mathrm{i}} ={r}^{\mathrm{1}+\mathrm{i}} \mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\theta} ={r}×{r}^{\mathrm{i}} ×\frac{\mathrm{1}}{\mathrm{e}^{\theta} }×\mathrm{e}^{\mathrm{i}\theta} =\frac{{r}}{\mathrm{e}^{\theta} }\mathrm{e}^{\mathrm{i}\:\left(\theta+\mathrm{ln}\:{r}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{i}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{e}^{−\mathrm{i}\frac{\pi}{\mathrm{4}}} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{i}\right){x}^{\mathrm{1}+\mathrm{i}} =\frac{\sqrt{\mathrm{2}}{r}}{\mathrm{2e}^{\theta} }\mathrm{e}^{\mathrm{i}\left(\theta+\mathrm{ln}\:{r}\:−\frac{\pi}{\mathrm{4}}\right)} \\ $$
