Menu Close

x-iy-3-6-2-7-i-1-7-i-find-x-y-

Tinku Tara 0 Comments
Pin




Question Number 129809 by mohammad17 last updated on 19/Jan/21
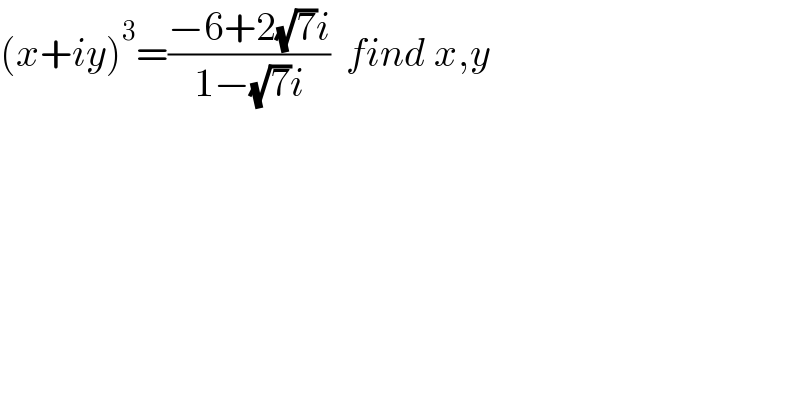
(x+iy)^3 =((−6+2(√7)i)/(1−(√7)i)) find x,y
$$\left({x}+{iy}\right)^{\mathrm{3}} =\frac{−\mathrm{6}+\mathrm{2}\sqrt{\mathrm{7}}{i}}{\mathrm{1}−\sqrt{\mathrm{7}}{i}}\:\:{find}\:{x},{y} \\ $$
Answered by Olaf last updated on 20/Jan/21
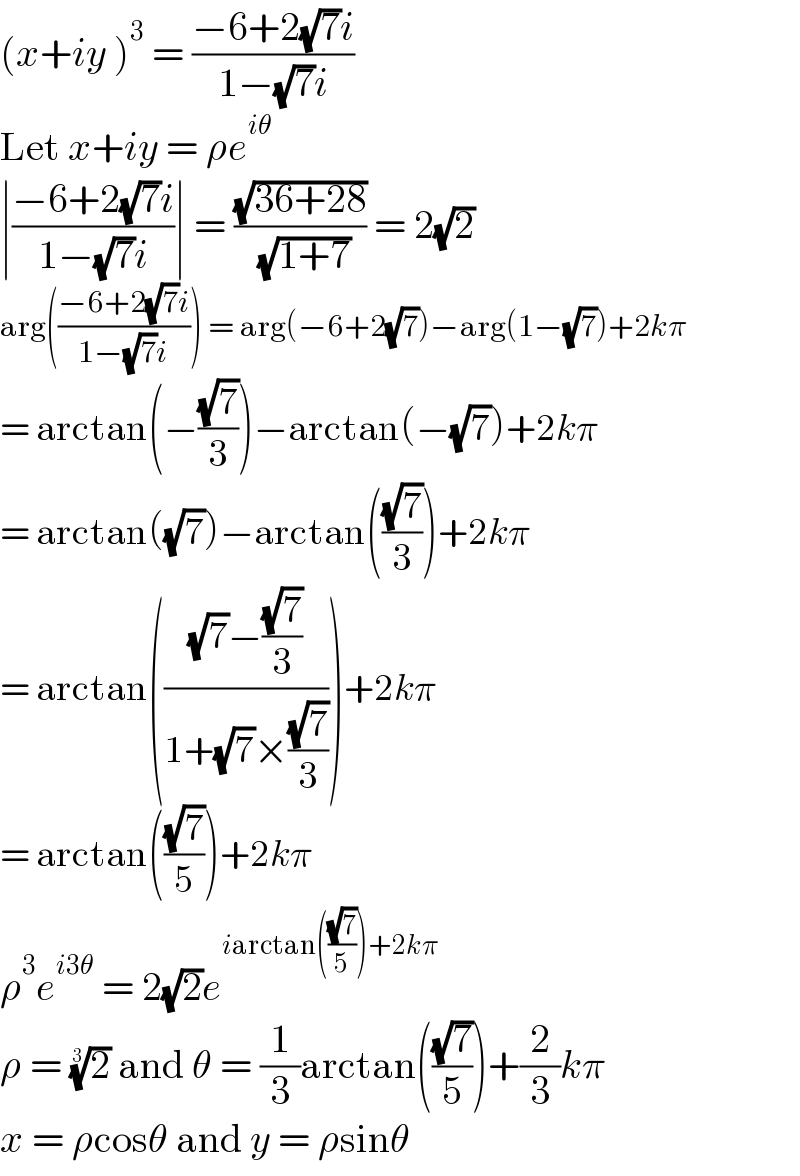
(x+iy )^3 = ((−6+2(√7)i)/(1−(√7)i)) Let x+iy = ρe^(iθ) ∣((−6+2(√7)i)/(1−(√7)i))∣ = ((√(36+28))/( (√(1+7)))) = 2(√2) arg(((−6+2(√7)i)/(1−(√7)i))) = arg(−6+2(√7))−arg(1−(√7))+2kπ = arctan(−((√7)/3))−arctan(−(√7))+2kπ = arctan((√7))−arctan(((√7)/3))+2kπ = arctan((((√7)−((√7)/3))/(1+(√7)×((√7)/3))))+2kπ = arctan(((√7)/5))+2kπ ρ^3 e^(i3θ) = 2(√2)e^(iarctan(((√7)/5))+2kπ) ρ = (2)^(1/3) and θ = (1/3)arctan(((√7)/5))+(2/3)kπ x = ρcosθ and y = ρsinθ
$$\left({x}+{iy}\:\right)^{\mathrm{3}} \:=\:\frac{−\mathrm{6}+\mathrm{2}\sqrt{\mathrm{7}}{i}}{\mathrm{1}−\sqrt{\mathrm{7}}{i}} \\ $$$$\mathrm{Let}\:{x}+{iy}\:=\:\rho{e}^{{i}\theta} \\ $$$$\mid\frac{−\mathrm{6}+\mathrm{2}\sqrt{\mathrm{7}}{i}}{\mathrm{1}−\sqrt{\mathrm{7}}{i}}\mid\:=\:\frac{\sqrt{\mathrm{36}+\mathrm{28}}}{\:\sqrt{\mathrm{1}+\mathrm{7}}}\:=\:\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\mathrm{arg}\left(\frac{−\mathrm{6}+\mathrm{2}\sqrt{\mathrm{7}}{i}}{\mathrm{1}−\sqrt{\mathrm{7}}{i}}\right)\:=\:\mathrm{arg}\left(−\mathrm{6}+\mathrm{2}\sqrt{\mathrm{7}}\right)−\mathrm{arg}\left(\mathrm{1}−\sqrt{\mathrm{7}}\right)+\mathrm{2}{k}\pi \\ $$$$=\:\mathrm{arctan}\left(−\frac{\sqrt{\mathrm{7}}}{\mathrm{3}}\right)−\mathrm{arctan}\left(−\sqrt{\mathrm{7}}\right)+\mathrm{2}{k}\pi \\ $$$$=\:\mathrm{arctan}\left(\sqrt{\mathrm{7}}\right)−\mathrm{arctan}\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{3}}\right)+\mathrm{2}{k}\pi \\ $$$$=\:\mathrm{arctan}\left(\frac{\sqrt{\mathrm{7}}−\frac{\sqrt{\mathrm{7}}}{\mathrm{3}}}{\mathrm{1}+\sqrt{\mathrm{7}}×\frac{\sqrt{\mathrm{7}}}{\mathrm{3}}}\right)+\mathrm{2}{k}\pi \\ $$$$=\:\mathrm{arctan}\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{5}}\right)+\mathrm{2}{k}\pi \\ $$$$\rho^{\mathrm{3}} {e}^{{i}\mathrm{3}\theta} \:=\:\mathrm{2}\sqrt{\mathrm{2}}{e}^{{i}\mathrm{arctan}\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{5}}\right)+\mathrm{2}{k}\pi} \\ $$$$\rho\:=\:\sqrt[{\mathrm{3}}]{\mathrm{2}}\:\mathrm{and}\:\theta\:=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arctan}\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{5}}\right)+\frac{\mathrm{2}}{\mathrm{3}}{k}\pi \\ $$$${x}\:=\:\rho\mathrm{cos}\theta\:\mathrm{and}\:{y}\:=\:\rho\mathrm{sin}\theta \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *